Introduction to Parallelisation
Overview
Teaching: 30 min
Exercises: 0 minQuestions
What is parallelisation?
Why is parallel programming important?
What are the different types of parallelism?
What are the common challenges in parallel programming?
Objectives
Understand the concept of parallelisation and its significance in improving performance.
Explore different types of parallelism, including shared memory parallelism.
Gain familiarity with the basics of OpenMP and how it enables shared memory parallelism.
Parallelisation is a technique that allows us to divide a complex computational task into smaller subtasks, enabling simultaneous execution and improving performance while reducing execution times. In this course, you will learn how to design parallel algorithms and write parallel programs using OpenMP. OpenMP, an abbreviation for “Open Multi-Processing,” is an application programming interface (API) that supports parallel programming in C, C++, and Fortran. It simplifies the development of multithreaded programs by incorporating compiler directives, library routines, and environment variables in a simple and portable manner. However, before we dive into programming with OpenMP, let’s establish a strong foundation by exploring key concepts that are essential to parallel programming. These concepts will provide us with the necessary knowledge and understanding as we progress through the upcoming episodes.
Parallelisation in A Nutshell
At some point in your career, you’ve probably asked the question “How can I make my code run faster?”. Of course, the answer to this question will depend sensitively on your specific situation, but here are a few approaches you might try doing:
- Optimize the code.
- Move computationally demanding parts of the code from an interpreted language (Python, Ruby, etc.) to a compiled language (C/C++, Fortran, Julia, Rust, etc.).
- Use better theoretical methods that require less computation for the same accuracy.
Each of the above approaches is intended to reduce the total amount of work required by the computer to run your code. A different strategy for speeding up codes is parallelisation, in which you split the computational work among multiple processing units that labor simultaneously. The “processing units” might include central processing units (CPUs), graphics processing units (GPUs), vector processing units (VPUs), or something similar.
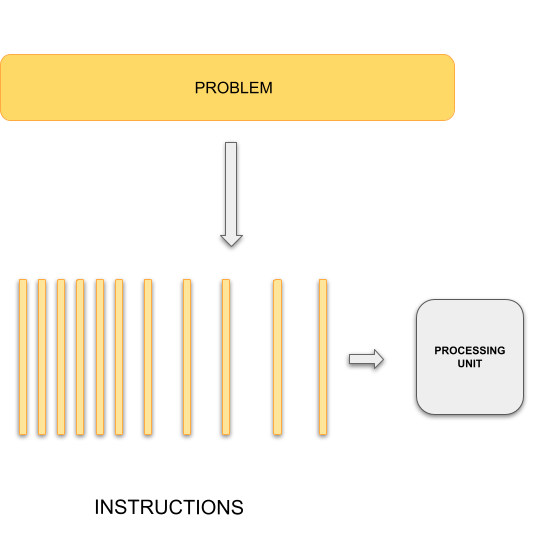
Sequential Computing
|
Parallel Computing 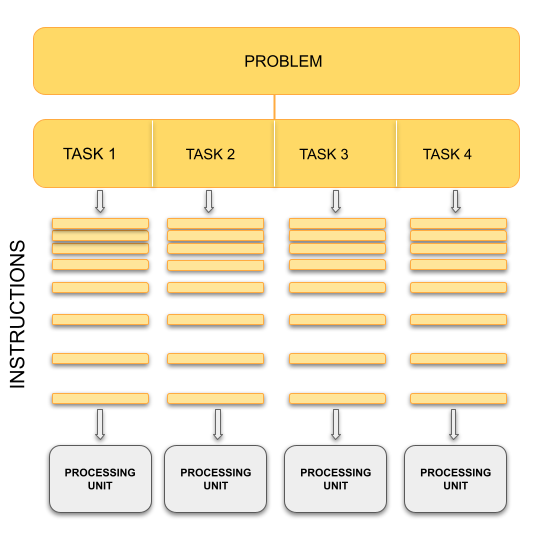
|
In general, typical programming assumes that computers execute one operation at a time in the sequence specified by your program code. At any time step, the computer’s CPU core will be working on one particular operation from the sequence. In other words, a problem is broken into discrete series of instructions that are executed one for another. Therefore only one instruction can execute at any moment in time. We will call this traditional style of sequential computing.
In contrast, with parallel computing we will now be dealing with multiple CPU cores that each are independently and simultaneously working on a series of instructions. This can allow us to do much more at once, and therefore get results more quickly than if only running an equivalent sequential program. The act of changing sequential code to parallel code is called parallelisation.
Analogy
The basic concept of parallel computing is simple to understand: we divide our job in tasks that can be executed at the same time so that we finish the job in a fraction of the time that it would have taken if the tasks are executed one by one.
Suppose that we want to paint the four walls in a room. This is our problem. We can divide our problem in 4 different tasks: paint each of the walls. In principle, our 4 tasks are independent from each other in the sense that we don’t need to finish one to start another. However, this does not mean that the tasks can be executed simultaneously or in parallel. It all depends on on the amount of resources that we have for the tasks.
If there is only one painter, they could work for a while in one wall, then start painting another one, then work a little bit on the third one, and so on. The tasks are being executed concurrently but not in parallel and only one task is being performed at a time. If we have 2 or more painters for the job, then the tasks can be performed in parallel.
Key idea
In our analogy, the painters represent CPU cores in the computers. The number of CPU cores available determines the maximum number of tasks that can be performed in parallel. The number of concurrent tasks that can be started at the same time, however is unlimited.
Splitting the problem into computational tasks across different processors and running them all at once may conceptually seem like a straightforward solution to achieve the desired speed-up in problem-solving. However, in practice, parallel programming involves more than just task division and introduces various complexities and considerations.
Let’s consider a scenario where you have a single CPU core, associated RAM (primary memory for faster data access), hard disk (secondary memory for slower data access), input devices (keyboard, mouse), and output devices (screen).
Now, imagine having two or more CPU cores. Suddenly, you have several new factors to take into account:
- If there are two cores, there are two possibilities: either these cores share the same RAM (shared memory) or each core has its own dedicated RAM (private memory).
- In the case of shared memory, what happens when two cores try to write to the same location simultaneously? This can lead to a race condition, which requires careful handling by the programmer to avoid conflicts.
- How do we divide and distribute the computational tasks among these cores? Ensuring a balanced workload distribution is essential for optimal performance.
- Communication between cores becomes a crucial consideration. How will the cores exchange data and synchronize their operations? Effective communication mechanisms must be established.
- After completing the tasks, where should the final results be stored? Should they reside in the storage of Core 1, Core 2, or a central storage accessible to both? Additionally, which core is responsible for displaying output on the screen?
These considerations highlight the interplay between parallel programming and memory. To efficiently utilize multiple CPU cores, we need to understand the different memory models—shared memory and distributed memory- as well as the concepts of processes and threads that form the foundation of parallel computing that play a crucial role in achieving optimal parallel execution.
To address the challenges that arise when parallelising programs across multiple cores and achieve efficient use of available resources, parallel programming frameworks like OpenMP and MPI (Message Passing Interface) come into play. These frameworks provide tools, libraries, and methodologies to handle memory management, workload distribution, communication, and synchronization in parallel environments.
Now, let’s take a brief look at these fundamental concepts and explore the differences between OpenMP and MPI, setting the stage for a deeper understanding of OpenMP for the next episode.
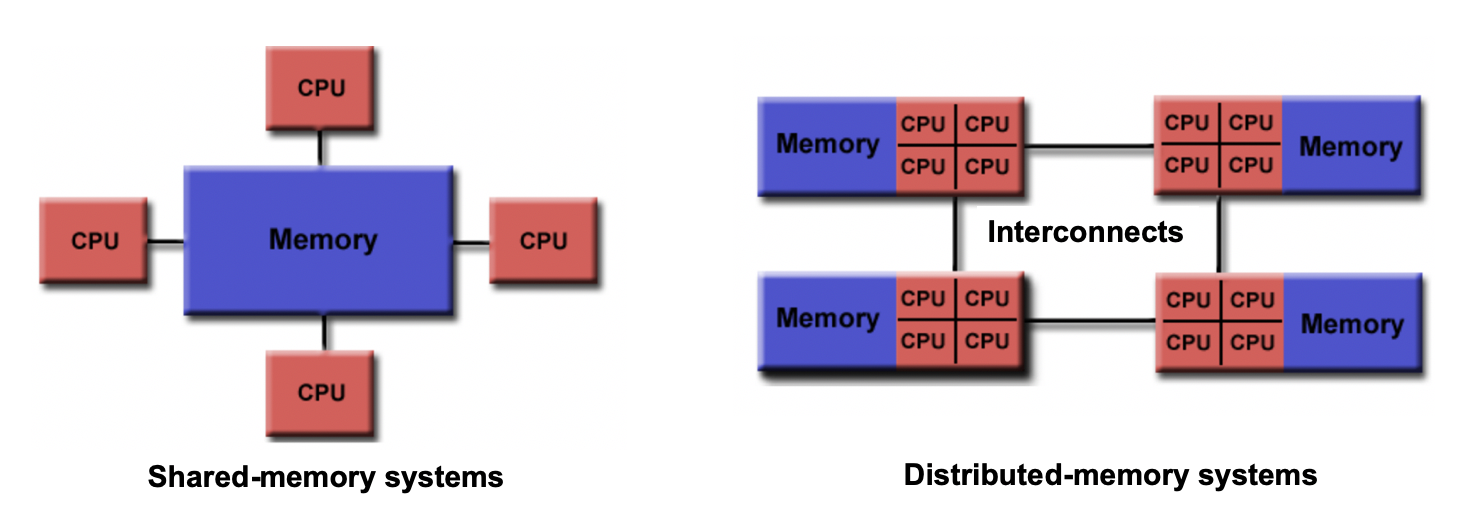
Shared vs Distributed Memory
Shared memory refers to a memory model where multiple processors can directly access and modify the same memory space. Changes made by one processor are immediately visible to all other processors. Shared memory programming models, like OpenMP, simplify parallel programming by providing mechanisms for sharing and synchronizing data.
Distributed memory, on the other hand, involves memory resources that are physically separated across different computers or nodes in a network. Each processor has its own private memory, and explicit communication is required to exchange data between processors. Distributed memory programming models, such as MPI, facilitate communication and synchronization in this memory model.
The choice between shared memory and distributed memory models depends on the nature of the problem and the available computing resources. Shared memory parallelism is well-suited for problems that can be efficiently divided into smaller tasks and where the coordination and communication overhead are relatively low. Distributed memory parallelism shines in scenarios where the problem size exceeds the capabilities of a single machine, and computation needs to be distributed across multiple nodes.
Differences/Advantages/Disadvantages of Shared and Distributed Memory
- Accessibility: Shared memory allows direct access to the same memory space by all processors, while distributed memory requires explicit communication for data exchange between processors.
- Memory Scope: Shared memory provides a global memory space, enabling easy data sharing and synchronization. In distributed memory, each processor has its own private memory space, requiring explicit communication for data sharing.
- Memory Consistency: Shared memory ensures immediate visibility of changes made by one processor to all other processors. Distributed memory requires explicit communication and synchronization to maintain data consistency across processors.
- Scalability: Shared memory systems are typically limited to a single computer or node, whereas distributed memory systems can scale to larger configurations with multiple computers and nodes.
- Programming Complexity: Shared memory programming models offer simpler constructs and require less explicit communication compared to distributed memory models. Distributed memory programming involves explicit data communication and synchronization, adding complexity to the programming process.
Analogy
Imagine that all workers have to obtain their paint from a central dispenser located at the middle of the room. If each worker is using a different colour, then they can work asynchronously. However, if they use the same colour, and two of them run out of paint at the same time, then they have to synchronise to use the dispenser — one should wait while the other is being serviced.
Now let’s assume that we have 4 paint dispensers, one for each worker. In this scenario, each worker can complete their task totally on their own. They don’t even have to be in the same room, they could be painting walls of different rooms in the house, in different houses in the city, and different cities in the country. We need, however, a communication system in place. Suppose that worker A, for some reason, needs a colour that is only available in the dispenser of worker B, they must then synchronise: worker A must request the paint of worker B and worker B must respond by sending the required colour.
Key Idea
In our analogy, the paint dispenser represents access to the memory in your computer. Depending on how a program is written, access to data in memory can be synchronous or asynchronous. For the different dispensers case for your workers, however, think of the memory distributed on each node/computer of a cluster.
Processes
A process refers to an individual running instance of a software program. Each process operates independently and possesses its own set of resources, such as memory space and open files. As a result, data within one process remains isolated and cannot be directly accessed by other processes.
In parallel programming, the objective is to achieve parallel execution by simultaneously running coordinated processes. This naturally introduces the need for communication and data sharing among them. To facilitate this, parallel programming models like MPI come into effect. MPI provides a comprehensive set of libraries, tools, and methodologies that enable processes to exchange messages, coordinate actions, and share data, enabling parallel execution across a cluster or network of machines.
Threads
A thread is an execution unit within a process. Unlike processes, threads operate within the context of a single process and share the same memory and resources. Threads can be thought of as separate points of execution within a program, capable of performing tasks concurrently.
In a single-threaded program, there is only one thread of execution within a process and it follows a sequential flow, where each instruction is executed one after another. In a multi-threaded program, however, multiple threads of execution exist within a single process. These threads can access and share the same data and resources, enabling more efficient and faster parallel programming.
One advantage of using threads is that they can be easier to work with compared to processes when it comes to parallel programming. When incorporating threads, especially with frameworks like OpenMP, modifying a program becomes simpler. This ease of use stems from the fact that threads operate within the same process and can directly access shared data, eliminating the need for complex inter-process communication mechanisms required by MPI. However, it’s important to note that threads within a process are limited to a single computer. While they provide an effective means of utilizing multiple CPU cores on a single machine, they cannot extend beyond the boundaries of that computer.
Analogy
Let’s go back to our painting 4 walls examples with a team of workers. Each painter represents a “process” (an individual instance of a program), and they share the same painting tools and materials. Now, let’s focus on the painters’ arms. Each arm can be seen as a “thread”, capable of performing independent actions and working on different sections of the wall simultaneously. Just as the painters coordinate their movements to avoid conflicts and overlap, threads in a program coordinate their execution to ensure synchronization and efficient use of shared resources.
In our painting analogy, a single-threaded program can be compared to a single painter working alone to paint the walls of a room. The painter performs each stroke of the brush in a sequential manner, completing the painting task step by step.
Now, let’s introduce the concept of multiple threads within a process. In our painting analogy, imagine the team of painters expanding their operations. Each painter still represents a process, but now they have multiple threads of execution represented by their arms. Each arm can work independently, allowing different sections of the wall to be painted simultaneously.
Parallel Paradigms
Thinking back to shared vs distributed memory models, how to achieve a parallel computation is divided roughly into two paradigms. Let’s set both of these in context:
- In a shared memory model, a data parallelism paradigm is typically used, as employed by OpenMP: the same operations are performed simultaneously on data that is shared across each parallel operation. Parallelism is achieved by how much of the data a single operation can act on.
- In a distributed memory model, a message passing paradigm is used, as employed by MPI: each CPU (or core) runs an independent program. Parallelism is achieved by receiving data which it doesn’t have, conducting some operations on this data, and sending data which it has.
This division is mainly due to historical development of parallel architectures: the first one follows from shared memory architecture like SMP (Shared Memory Processors) and the second from distributed computer architecture. A familiar example of the shared memory architecture is GPU (or multi-core CPU) architecture, and an example of the distributed computing architecture is a cluster of distributed computers. Which architecture is more useful depends on what kind of problems you have. Sometimes, one has to use both!
Consider a simple loop which can be sped up if we have many cores for illustration:
for(i=0; i<N; i++) {
a[i] = b[i] + c[i];
}
If we have N or more cores, each element of the loop can be computed in
just one step (for a factor of \(N\) speed-up). Let’s look into both paradigms in a little more detail, and focus on key characteristics.
1. Data Parallelism Paradigm
To understand what data parallelism means, let’s consider the following bit of OpenMP code which parallelizes the above loop:
#pragma omp parallel for for(i=0; i<N; i++) { a[i] = b[i] + c[i]; }Parallelization achieved by just one additional line,
#pragma omp parallel for, handled by the preprocessor in the compile stage, where the compiler “calculates” the data address off-set for each core and lets each one compute on a part of the whole data. This approach provides a convenient abstraction, and hides the underlying parallelisation mechanisms.Here, the catch word is shared memory which allows all cores to access all the address space. We’ll be looking into OpenMP later in this course. In Python, process-based parallelism is supported by the multiprocessing module.
2. Message Passing Paradigm
In the message passing paradigm, each processor runs its own program and works on its own data. To work on the same problem in parallel, they communicate by sending messages to each other. Again using the above example, each core runs the same program over a portion of the data. For example, using this paradigm to parallelise the above loop instead:
for(i=0; i<m; i++) { a[i] = b[i] + c[i]; }
- Other than changing the number of loops from
Ntom, the code is exactly the same.mis the reduced number of loops each core needs to do (if there areNcores,mis 1 (=N/N)). But the parallelization by message passing is not complete yet. In the message passing paradigm, each core operates independently from the other cores. So each core needs to be sent the correct data to compute, which then returns the output from that computation. However, we also need a core to coordinate the splitting up of that data, send portions of that data to other cores, and to receive the resulting computations from those cores.Summary
In the end, both data parallelism and message passing logically achieve the following:
Therefore, each rank essentially operates on its own set of data, regardless of paradigm. In some cases, there are advantages to combining data parallelism and message passing methods together, e.g. when there are problems larger than one GPU can handle. In this case, data parallelism is used for the portion of the problem contained within one GPU, and then message passing is used to employ several GPUs (each GPU handles a part of the problem) unless special hardware/software supports multiple GPU usage.
Algorithm Design
Designing a parallel algorithm that determines which of the two paradigms above one should follow rests on the actual understanding of how the problem can be solved in parallel. This requires some thought and practice.
To get used to “thinking in parallel”, we discuss “Embarrassingly Parallel” (EP) problems first and then we consider problems which are not EP problems.
Embarrassingly Parallel Problems
Problems which can be parallelized most easily are EP problems, which occur in many Monte Carlo simulation problems and in many big database search problems. In Monte Carlo simulations, random initial conditions are used in order to sample a real situation. So, a random number is given and the computation follows using this random number. Depending on the random number, some computation may finish quicker and some computation may take longer to finish. And we need to sample a lot (like a billion times) to get a rough picture of the real situation. The problem becomes running the same code with a different random number over and over again! In big database searches, one needs to dig through all the data to find wanted data. There may be just one datum or many data which fit the search criterion. Sometimes, we don’t need all the data which satisfies the condition. Sometimes, we do need all of them. To speed up the search, the big database is divided into smaller databases, and each smaller databases are searched independently by many workers!
Queue Method
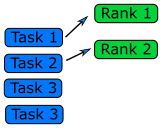
Each worker will get tasks from a predefined queue (a random number in a Monte Carlo problem and smaller databases in a big database search problem). The tasks can be very different and take different amounts of time, but when a worker has completed its tasks, it will pick the next one from the queue.
In an MPI code, the queue approach requires the ranks to communicate what they are doing to all the other ranks, resulting in some communication overhead (but negligible compared to overall task time).
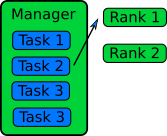
Manager / Worker Method
The manager / worker approach is a more flexible version of the queue method. We hire a manager to distribute tasks to the workers. The manager can run some complicated logic to decide which tasks to give to a worker. The manager can also perform any serial parts of the program like generating random numbers or dividing up the big database. The manager can become one of the workers after finishing managerial work.
In an MPI implementation, the main function will usually contain an
ifstatement that determines whether the rank is the manager or a worker. The manager can execute a completely different code from the workers, or the manager can execute the same partial code as the workers once the managerial part of the code is done. It depends on whether the managerial load takes a lot of time to finish or not. Idling is a waste in parallel computing!Because every worker rank needs to communicate with the manager, the bandwidth of the manager rank can become a bottleneck if administrative work needs a lot of information (as we can observe in real life). This can happen if the manager needs to send smaller databases (divided from one big database) to the worker ranks. This is a waste of resources and is not a suitable solution for an EP problem. Instead, it’s better to have a parallel file system so that each worker rank can access the necessary part of the big database independently.
General Parallel Problems (Non-EP Problems)
In general not all the parts of a serial code can be parallelized. So, one needs to identify which part of a serial code is parallelizable. In science and technology, many numerical computations can be defined on a regular structured data (e.g., partial differential equations in a 3D space using a finite difference method). In this case, one needs to consider how to decompose the domain so that many cores can work in parallel.
Domain Decomposition
When the data is structured in a regular way, such as when simulating atoms in a crystal, it makes sense to divide the space into domains. Each rank will handle the simulation within its own domain.
Many algorithms involve multiplying very large matrices. These include finite element methods for computational field theories as well as training and applying neural networks. The most common parallel algorithm for matrix multiplication divides the input matrices into smaller submatrices and composes the result from multiplications of the submatrices. If there are four ranks, the matrix is divided into four submatrices.
\[A = \left[ \begin{array}{cc}A_{11} & A_{12} \\ A_{21} & A_{22}\end{array} \right]\] \[B = \left[ \begin{array}{cc}B_{11} & B_{12} \\ B_{21} & B_{22}\end{array} \right]\] \[A \cdot B = \left[ \begin{array}{cc}A_{11} \cdot B_{11} + A_{12} \cdot B_{21} & A_{11} \cdot B_{12} + A_{12} \cdot B_{22} \\ A_{21} \cdot B_{11} + A_{22} \cdot B_{21} & A_{21} \cdot B_{12} + A_{22} \cdot B_{22}\end{array} \right]\]If the number of ranks is higher, each rank needs data from one row and one column to complete its operation.
Load Balancing
Even if the data is structured in a regular way and the domain is decomposed such that each core can take charge of roughly equal amounts of the sub-domain, the work that each core has to do may not be equal. For example, in weather forecasting, the 3D spatial domain can be decomposed in an equal portion. But when the sun moves across the domain, the amount of work is different in that domain since more complicated chemistry/physics is happening in that domain. Balancing this type of loads is a difficult problem and requires a careful thought before designing a parallel algorithm.
Serial and Parallel Regions
Identify the serial and parallel regions in the following algorithm:
vector_1[0] = 1; vector_1[1] = 1; for i in 2 ... 1000 vector_1[i] = vector_1[i-1] + vector_1[i-2]; for i in 0 ... 1000 vector_2[i] = i; for i in 0 ... 1000 vector_3[i] = vector_2[i] + vector_1[i]; print("The sum of the vectors is.", vector_3[i]);Solution
serial | vector_0[0] = 1; | vector_1[1] = 1; | for i in 2 ... 1000 | vector_1[i] = vector_1[i-1] + vector_1[i-2]; parallel | for i in 0 ... 1000 | vector_2[i] = i; parallel | for i in 0 ... 1000 | vector_3[i] = vector_2[i] + vector_1[i]; | print("The sum of the vectors is.", vector_3[i]); The first and the second loop could also run at the same time.In the first loop, every iteration depends on data from the previous two. In the second two loops, nothing in a step depends on any of the other steps, and therefore can be parallelised.
Key Points
Parallelization involves dividing complex computational tasks into smaller subtasks that can be executed simultaneously, leading to improved performance and reduced execution times.
Parallel programming enables algorithms to leverage parallel hardware architectures, such as multi-core CPUs and GPUs, to achieve faster computations.
OpenMP is an essential parallel programming API that simplifies the development of multithreaded programs by incorporating compiler directives, library routines, and environment variables in a portable manner.
Shared memory parallelism is a fundamental concept in OpenMP, where threads share memory and work together to solve computational problems effectively.
Introduction to OpenMP
Overview
Teaching: 10 min
Exercises: 0 minQuestions
What is OpenMP?
How does OpenMP work?
Why the researches should prefer OpenMP over POSIX?
Objectives
Learn what OpenMP is
Understand how to use the OpenMP API
Learn how to compile and run OpenMP applications
Understand the difference between OpenMP and low level threading APIs
What is OpenMP?
OpenMP is an industry-standard API specifically designed for parallel programming in shared memory environments. It supports programming in languages such as C, C++, and Fortran. OpenMP is an open source, industry-wide initiative that benefits from collaboration among hardware and software vendors, governed by the OpenMP Architecture Review Board (OpenMP ARB).
An OpenMP Timeline
The timeline provides an overview of OpenMP’s evolution until 2014, with significant advancements occurring thereafter. Notably, OpenMP 5.0 marked a significant step in 2018, followed by the latest iteration, OpenMP 5.2, which was released in November 2021.
How does it work?
OpenMP allows programmers to identify and parallelize sections of code, enabling multiple threads to execute them concurrently. This concurrency is achieved using a shared-memory model, where all threads can access a common memory space and communicate through shared variables.
To understand how OpenMP orchestrates this parallel execution, let’s explore the fork-join model it employs. Think of your program as a team with a leader (the master thread) and workers (the slave threads). When your program starts, the leader thread takes the lead. It identifies parts of the code that can be done at the same time and marks them. These marked parts are like tasks to be completed by the workers. The leader then gathers a group of helper threads, and each helper tackles one of these marked tasks. Each worker thread works independently, taking care of its task. Once all the workers are done, they come back to the leader, and the leader continues with the rest of the program.
In simpler terms, when your program finds a special “parallel” section, it’s like the leader telling the workers to split up and work on different tasks together (that’s the “fork” part). After finishing their tasks, these workers come back to the leader, allowing the leader to move forward (that’s the “join” part). This teamwork approach helps OpenMP speed up tasks and get things done faster.
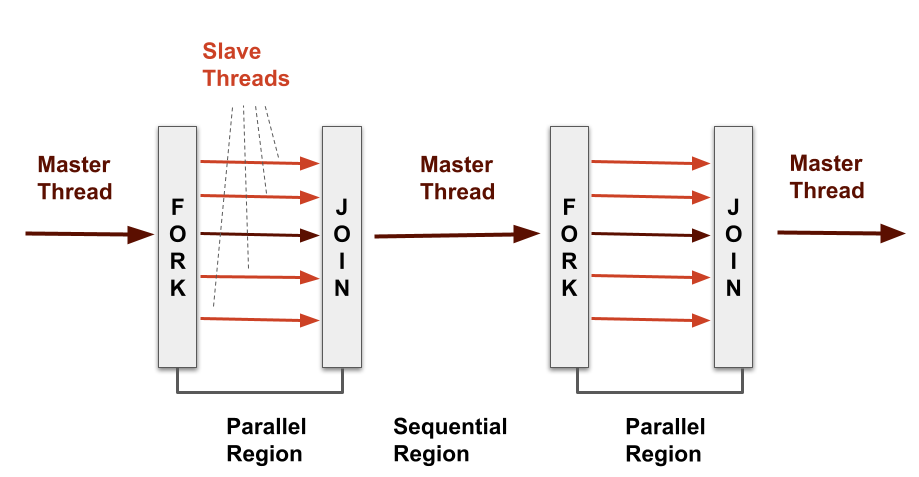
OpenMP consists of three key components that enable parallel programming using threads:
- Compiler directives: OpenMP makes use of special code markers known as compiler directives to indicate to the compiler when and how to parallelise various sections of code. These directives are prefixed with
#pragma omp, and mark sections of code to be executed concurrently by multiple threads. - Runtime Library Routines: These are predefined functions provided by the OpenMP runtime library. They allow you to control the behavior of threads, manage synchronization, and handle parallel execution. For example, we can use the function
omp_get_thread_num()to obtain the unique identifier of the calling thread. - Environment Variables: These are settings that can be adjusted to influence the behavior of the OpenMP runtime. They provide a way to fine-tune the parallel execution of your program. Setting OpenMP environment variables is typically done similarly to other environment variables for your system. For instance, you can adjust the number of threads to use for a program you are about to execute by specifying the value in the
OMP_NUM_THREADSenvironment variable.
Running a Code with OpenMP
Before we delve into specifics of writing code that uses OpenMP, let’s first look at how we compile and run an example “Hello World!” OpenMP program that prints this to the console.
Save the following code in hello_world_omp.c:
#include <stdio.h>
#include <omp.h>
int main() {
#pragma omp parallel
{
printf("Hello World!\n");
}
}
You’ll want to compile it using a standard compiler such as gcc. To enable the creation of multi-threaded code based on OpenMP directives, pass the -fopenmp flag to the compiler. This flag indicates that you’re compiling an OpenMP program:
gcc hello_world_omp.c -o hello_world_omp -fopenmp
Before we run the code we also need to indicate how many threads we wish the program to use.
One way to do this is to specify this using the OMP_NUM_THREADS environment variable, e.g.
export OMP_NUM_THREADS=4
Now you can run it just like any other program using the following command:
./hello_world_omp
When you execute the OpenMP program,
it will display ‘Hello World!’ multiple times according to the value we entered in OMP_NUM_THREADS,
with each thread in the parallel region executing the printf statement concurrently:
Hello World!
Hello World!
Hello World!
Hello World!
OpenMP vs. Low-Level Threading APIs (POSIX Threads)
When it comes to parallel programming with threads, there are two main ways to tackle it: the user-friendly OpenMP and the more intricate Low-Level Threading APIs. In this context, Low-Level Threading APIs, refer to interfaces like the Portable Operating System Interface (POSIX), which defines a set of standard functions and interfaces for interacting with operating systems. Each approach has its own advantages and considerations, so let’s break them down in simpler terms:
OpenMP serves as a gentle introduction to parallel programming. It offers an easy way to parallelize your code without delving into complex technicalities. This makes it ideal for beginners or anyone seeking a straightforward approach. It’s like choosing a reliable car that gets you from point A to point B comfortably.
Advantages of OpenMP:
- User-Friendly: OpenMP requires minimal code adjustments, making it a friendly choice for newcomers.
- Automated Work Distribution: It divides tasks among threads, ensuring balanced workloads.
- Wider Applicability: OpenMP functions across different systems and programming languages.
For instance, consider a scenario where you have a task that involves doing the same thing over and over again, like processing a bunch of images. With OpenMP, you can split up the work among different threads, so they each handle a part of the task at the same time.
Now, imagine you’re a master chef who wants complete control over every ingredient and spice in a recipe. That’s what Low-Level Threading APIs, like POSIX, offer – a lot of control over threads and how they work together. But this kind of control requires a bit more knowledge and effort.
Benefits of Low-Level Threading APIs:
- Full Control: These APIs allow you to customize every aspect of threads, but it requires a deeper understanding.
- Better Performance: If you know exactly what you’re doing, you can make things run faster and more efficiently.
- Flexible Solutions: You can create solutions that perfectly match your unique needs.
Let’s say you’re building a game where players from different parts of the world can interact with each other in real-time. Here, using POSIX threading would give you the control you need to manage these interactions smoothly and avoid any weird glitches.
Choosing the Right Framework
When deciding between OpenMP and Low-Level Threading APIs like POSIX for your parallel programming needs, several factors come into play:
| Aspect | OpenMP | Low-Level Threading APIs like POSIX |
|---|---|---|
| Ease of Use | User-friendly, higher-level abstractions | Lower-level, more manual management of threads |
| Parallelism Scope | Parallel regions, loops, tasks | Usually limited to thread creation and synchronization |
| Portability | Portable across different systems | Depends on system-specific implementation |
| Abstraction Level | Higher-level constructs and directives | Direct interaction with system-level threading |
| GPU Offloading Support | Supports offloading work to GPUs | Typically lacks built-in support for GPU offloading |
| Maintenance Complexity | Easier maintenance due to higher abstractions | Requires more low-level management |
| Performance Optimization | May offer automatic optimization | Requires manual tuning for performance |
| Common Usage | Widely used in research and industry | Less common due to lower-level complexities |
In summary, OpenMP offers a more user-friendly and productive experience, especially for researchers who want to focus on problem-solving rather than thread management. Additionally, its support for GPU # offloading enhances performance in certain scenarios. On the other hand, Low-Level Threading APIs like POSIX provide greater control and are suitable for those with a solid grasp of system-level programming.
Key Points
OpenMP is an industry-standard API for parallel programming in shared memory environments.
It supports C, C++, and Fortran and is governed by the OpenMP ARB.
OpenMP follows the fork-join model, using master and slave threads for parallel tasks.
Compiler directives guide the compiler to create parallel code, e.g.,
#pragma omp parallel.Runtime library routines offer predefined functions for thread control and synchronization.
Environment variables fine-tune OpenMP runtime behavior.
To compile and run OpenMP programs, include the
<omp.h>header, compile with-fopenmpflag, and execute the compiled binary.OpenMP is user-friendly, automating thread distribution across systems.
Both OpenMP and Low-Level Threading APIs provide effective parallel programming options. The choice depends on factors like ease of use, control, and performance optimization.
Writing Parallel Applications with OpenMP
Overview
Teaching: 15 min
Exercises: 0 minQuestions
How can I use OpenMP within a program?
Objectives
Learn how to parallelise work in a program using OpenMP
Describe two major OpenMP pragma directives
Define and use a parallel region in our code
Use OpenMP library functions to obtain the number of available threads and the current thread identifier
Describe the classes of visibility (or scoping) of variables between threads
Parallelise a for loop using OpenMP
Describe the different schedulers available for how OpenMP assigns loop iterations to threads
Change the scheduling behaviour for an example program
Using OpenMP in a Program
As we introduced in the last episode,
OpenMP directives are special comments indicated by #pragma omp statements that guide the compiler in creating parallel code.
They mark sections of code to be executed concurrently by multiple threads.
At a high level, the C/C++ syntax for pragma directives is as follows:
#pragma omp <name_of_directive> [ <optional_clause> ...]
Following a directive are multiple optional clauses, which are themselves C expressions and may contain other clauses, with any arguments to both directives and clauses enclosed in parentheses and separated by commas. For example:
#pragma omp a-directive a-clause(argument1, argument2)
OpenMP offers a number of directives for parallelisation, although the two we’ll focus on in this episode are:
- The
#pragma omp paralleldirective specifies a block of code for concurrent execution. - The
#pragma omp fordirective parallelizes loops by distributing loop iterations among threads.
Our First Parallelisation
For example, amending our previous example,
in the following we specify a specific block of code to run parallel threads,
using the OpenMP runtime routine omp_get_thread_num() to return
the unique identifier of the calling thread:
#include <stdio.h>
#include <omp.h>
int main() {
#pragma omp parallel
{
printf("Hello from thread %d\n", omp_get_thread_num());
}
}
So assuming you’ve specified OMP_NUM_THREADS as 4:
Hello from thread 0
Hello from thread 1
Hello from thread 3
Hello from thread 2
Although the output may not be in the same order,
since the order and manner in which these threads (and their printf statements) run is not guaranteed.
So in summary, simply by adding this directive we have accomplished a basic form of parallelisation.
What about Variables?
So how do we make use of variables across, and within, our parallel threads? Of particular importance in parallel programs is how memory is managed and how and where variables can be manipulated, and OpenMP has a number of mechanisms to indicate how they should be handled. Essentially, OpenMP provided two ways to do this for variables:
- Shared: holds a single instance for all threads to share
- Private: creates and hold a separate copy of the variable for each thread
For example, what if we wanted to hold the thread ID and the total number of threads within variables in the code block? Let’s start by amending the parallel code block to the following:
int num_threads = omp_get_num_threads();
int thread_id = omp_get_thread_num();
printf("Hello from thread %d out of %d\n", thread_id, num_threads);
Here, omp_get_num_threads() returns the total number of available threads.
If we recompile and re-run we should see:
Hello from thread 0 out of 4
Hello from thread 1 out of 4
Hello from thread 3 out of 4
Hello from thread 2 out of 4
OpenMP and C Scoping
Try printing out
num_threadsat the end of the program, after the#pragmacode block, and recompile. What happens? Is this what you expect?Solution
Since the variable is scoped only to the code block within the curly braces, as with any C code block,
num_threadsis no longer in scope and cannot be read.
Now by default, variables declared within parallel regions are private to each thread. But what about declarations outside of this block? For example:
...
int num_threads, thread_id;
#pragma omp parallel
{
num_threads = omp_get_num_threads();
thread_id = omp_get_thread_num();
printf("Hello from thread %d out of %d\n", thread_id, num_threads);
}
Which may seem on the surface to be correct.
However this illustrates a critical point about why we need to be careful.
Now the variables declarations are outside of the parallel block,
by default, variables are shared across threads, which means these variables can be changed at any time by
any thread, which is potentially dangerous.
So here, thread_id may hold the value for another thread identifier when it’s printed,
since there is an opportunity between it’s assignment and it’s access within printf to be changed in another thread.
This could be particularly problematic with a much larger data set and complex processing of that data,
where it might not be obvious that incorrect behaviour has happened at all,
and lead to incorrect results.
This is known as a race condition, and we’ll look into them in more detail in the next episode.
Observing the Race Condition
We can observe the race condition occurring by adding a sleep command between the
thread_idassignment and use. Add#include <unistd.h>to the top of your program, and afterthread_id’s assignment, addsleep(2);which will force the code to wait for 2 seconds before the variable is accessed, providing more opportunity for the race condition to occur. Hopefully you’ll then see the unwanted behaviour emerge, for example:Hello from thread 2 out of 4 Hello from thread 2 out of 4 Hello from thread 2 out of 4 Hello from thread 2 out of 4
But with our code, this makes variables potentially unsafe, since within a single thread, we are unable to guarantee their expected value. One approach to ensuring we don’t do this accidentally is to specify that there is no default behaviour for variable classification. We can do this by changing our directive to:
#pragma omp parallel default(none)
Now if we recompile, we’ll get an error mentioning that these variables aren’t specified for use within the parallel region:
hello_world_omp.c: In function 'main':
hello_world_omp.c:10:21: error: 'num_threads' not specified in enclosing 'parallel'
10 | num_threads = omp_get_num_threads();
| ~~~~~~~~~~~~^~~~~~~~~~~~~~~~~~~~~~~
hello_world_omp.c:8:13: note: enclosing 'parallel'
8 | #pragma omp parallel default(none)
| ^~~
hello_world_omp.c:11:19: error: 'thread_id' not specified in enclosing 'parallel'
11 | thread_id = omp_get_thread_num();
| ~~~~~~~~~~^~~~~~~~~~~~~~~~~~~~~~
hello_world_omp.c:8:13: note: enclosing 'parallel'
8 | #pragma omp parallel default(none)
| ^~~
So we now need to be explicit in every case for which variables are accessible within the block, and whether they’re private or shared:
#pragma omp parallel default(none) private(num_threads, thread_id)
So here, we ensure that each thread has its own private copy of these variables, which is now thread safe.
Parallel for Loops
A typical program uses for loops to perform many iterations of the same task,
and fortunately OpenMP gives us a straightforward way to parallelise them,
which builds on the use of directives we’ve learned so far.
...
int num_threads, thread_id;
omp_set_num_threads(4);
#pragma omp parallel for default(none) private(num_threads, thread_id)
for (int i = 1; i <= 10; i++)
{
num_threads = omp_get_num_threads();
thread_id = omp_get_thread_num();
printf("Hello from iteration %i from thread %d out of %d\n", i, thread_id, num_threads);
}
}
So essentially, very similar format to before, but here we use for in the pragma preceding a loop definition,
which will then assign 10 separate loop iterations across the 4 available threads.
Later in this episode we’ll explore the different ways in which OpenMP is able to schedule iterations from loops across these threads,
and how to specify different scheduling behaviours.
A Shortcut for Convenience
The
#pragma omp parallel foris actually equivalent to using two separate directives. For example:#pragma omp parallel { #pragma omp for for (int 1 = 1; 1 <=10; i++) { ... } }…is equivalent to:
#pragma omp parallel for for (int 1 = 1; 1 <=10; i++) { ... }In the first case,
#pragma omp parallelspawns a group of threads, whilst#pragma omp fordivides the loop iterations between them. But if you only need to do parallelisation within a single loop, the second case has you covered for convenience.
Note we also explicitly set the number of desired threads to 4, using the OpenMP omp_set_num_threads() function,
as opposed to the environment variable method.
Use of this function will override any value set in OMP_NUM_THREADS.
You should see something (but perhaps not exactly) like:
Hello from iteration 1 from thread 0 out of 4
Hello from iteration 2 from thread 0 out of 4
Hello from iteration 3 from thread 0 out of 4
Hello from iteration 4 from thread 1 out of 4
Hello from iteration 5 from thread 1 out of 4
Hello from iteration 6 from thread 1 out of 4
Hello from iteration 9 from thread 3 out of 4
Hello from iteration 10 from thread 3 out of 4
Hello from iteration 7 from thread 2 out of 4
Hello from iteration 8 from thread 2 out of 4
So with careful attention to variable scoping, using OpenMP to parallelise an existing loop is often quite straightforward. However, particularly with more complex programs, there are some aspects and potential pitfalls with OpenMP parallelisation we need to be aware of - such as race conditions - which we’ll explore in the next episode.
Calling Thread Numbering Functions Elsewhere?
Write, compile and run a simple OpenMP program that calls both
omp_get_num_threads()andomp_get_thread_num()outside of a parallel region, and prints the values received. What happens?Solution
omp_get_num_threads()will return 1 as you might expect, since there is only the primary thread active.
omp_get_thread_num()will return 0, which refers to the identifier for the primary thread, which is zero.
Using Schedulers
Whenever we use a parallel for, the iterations have to be split into smaller chunks so each thread has something to do. In most OpenMP implementations, the default behaviour is to split the iterations into equal sized chunks,
int CHUNK_SIZE = NUM_ITERATIONS / omp_get_num_threads();
If the amount of time it takes to compute each iteration is the same, or nearly the same, then this is a perfectly efficient way to parallelise the work. Each thread will finish its chunk at roughly the same time as the other thread. But if the work is imbalanced, even if just one thread takes longer per iteration, then the threads become out of sync and some will finish before others. This not only means that some threads will finish before others and have to wait until the others are done before the program can continue, but it’s also an inefficient use of resources to have threads/cores idling rather than doing work.
Fortunately, we can use other types of “scheduling” to control how work is divided between threads. In simple terms, a
scheduler is an algorithm which decides how to assign chunks of work to the threads. We can controller the scheduler we
want to use with the schedule directive:
#pragma omp parallel for schedule(SCHEDULER_NAME, OPTIONAL_ARGUMENT)
for (int i = 0; i < NUM_ITERATIONS; ++i) {
...
}
schedule takes two arguments: the name of the scheduler and an optional argument.
| Scheduler | Description | Argument | Uses |
|---|---|---|---|
| static | The work is divided into equal-sized chunks, and each thread is assigned a chunk to work on at compile time. | The chunk size to use (default: divides iterations into chunks of approx. equal size). | Best used when the workload is balanced across threads, where each iteration takes roughly the same amount of time. |
| dynamic | The work is divided into lots of small chunks, and each thread is dynamically assigned a new chunk with it finishes its current work. | The chunk size to use (default: 1). | Useful for loops with a workload imbalance, or variable execution time per iteration. |
| guided | The chunk sizes start large and decreases in size gradually. | The smallest chunk size to use (default: 1). | Most useful when the workload is unpredictable, as the scheduler can adapt the chunk size to adjust for any imbalance. |
| auto | The best choice of scheduling is chosen at run time. | - | Useful in all cases, but can introduce additional overheads whilst it decides which scheduler to use. |
| runtime | Determined at runtime by the OMP_SCHEDULE environment variable or omp_schedule pragma. |
- | - |
How the
autoScheduler WorksThe
autoscheduler lets the compiler or runtime system automatically decide the best way to distribute work among threads. This is really convenient because you don’t have to manually pick a scheduling method—the system handles it for you. It’s especially handy if your workload distribution is uncertain or changes a lot. But keep in mind that how wellautoworks can depend a lot on the compiler. Not all compilers optimize equally well, and there might be a bit of overhead as the runtime figures out the best scheduling method, which could affect performance in highly optimized code.The OpenMP documentation states that with
schedule(auto), the scheduling decision is left to the compiler or runtime system. So, how does the compiler make this decision? When using GCC, which is common in many environments including HPC, theautoscheduler often maps tostaticscheduling. This means it splits the work into equal chunks ahead of time for simplicity and performance.staticscheduling is straightforward and has low overhead, which often leads to efficient execution for many applications.However, specialized HPC compilers, like those from Intel or IBM, might handle
autodifferently. These advanced compilers can dynamically adjust the scheduling method during runtime, considering things like workload variability and specific hardware characteristics to optimize performance.So, when should you use
auto? It’s great during development for quick performance testing without having to manually adjust scheduling methods. It’s also useful in environments where the workload changes a lot, letting the runtime adapt the scheduling as needed. Whileautocan make your code simpler, it’s important to test different schedulers to see which one works best for your specific application.
Try Out Different Schedulers
Try each of the static and dynamic schedulers on the code below, which uses
sleepto mimic processing iterations that take increasing amounts of time to complete as the loop increases.staticis already specified, so replace this next withdynamic. Which scheduler is fastest?#include <unistd.h> #include <stdlib.h> #include <stdio.h> #include <omp.h> #define NUM_THREADS 4 #define NUM_ITERATIONS 8 int main ( ) { int i; double start = omp_get_wtime(); #pragma omp parallel for num_threads(NUM_THREADS) schedule(static) for (i = 0; i < NUM_ITERATIONS; i++) { sleep(i); printf("Thread %d finished iteration %d\n", omp_get_thread_num(), i); } double end = omp_get_wtime(); printf("Total time for %d reps = %f\n", NUM_ITERATIONS, end - start); }Try out the different schedulers and see how long it takes to finish the loop. Which scheduler was best?
Solution
You should see something like:
Static: Total time for 8 reps = 13.003299 Dynamic: Total time for 8 reps = 10.007052Here we can see that
dynamicis the fastest, which is better with iterations taking differing amounts of time. But note there is an overhead to using dynamic scheduling, threads that complete need to stop and await a new value to process from a next iteration.With a dynamic scheduler, the default chunk size is 1. What happens if specify a chunk size of 2, i.e.
scheduler(dynamic, 2)?Solution
Dynamic: Total time for 16 reps = 13.004029So here, we now see approximately the same results. By increasing the chunk size, the dynamic scheduler behaves more like the static one, since the workload for static would have the same chunk size calculated to be 2 (
NUM_ITERATIONS / NUM_THREADS = CHUNK_SIZE,8 / 4 = 2).
A Matter of Convenience
We’ve seen that we can amend our code directly to use different schedulers, but when testing our code with each of them editing and recompiling can become tedious. Fortunately we can use the
OMP_SCHEDULEenvironment variable to specify the scheduler instead, as well as the chunk size, so we don’t need to recompile.Edit your code to specify
runtimeas the scheduler, i.e.scheduler(runtime), recompile, then set the environment variable in turn to each scheduler, e.g.export OMP_SCHEDULE=dynamicThen rerun. Try it with different chunk sizes too, e.g.:
export OMP_SCHEDULE=static,1So much more convenient!
Key Points
Use
#pragma omp parallelto define a parallel code sectionThere are two types of variable scoping for parallel regions - shared (variables are shared across threads) and private (threads have their own copy of a variable separate to those of other threads).
To avoid ambiguous code behaviour, it is good practice to explicitly default to a
nonevariable sharing policy between thread, and define exceptions explicitly.Using
#pragma omp parallel foris a shorter way of defining anomp parallelsection and aomp parallel forwithin it.Using the library functions
omp_get_num_threads()andomp_get_thread_num()outside of a parallel region will return 1 and 0 respectively.There are 5 different scheduling methods - static, dynamic, guided, auto, and runtime.
We can use the
OMP_SCHEDULEenvironment variable to define a scheduler and chunk size that is used by theruntimescheduler.
Synchronisation and Race Conditions
Overview
Teaching: 0 min
Exercises: 0 minQuestions
Why do I need to worry about thread synchronisation?
What is a race condition?
Objectives
Understand what thread synchronisation is
Understand what a race condition is
Learn how to control thread synchronisation
Learn how to avoid errors caused by race conditions
In the previous episode, we saw how to use parallel regions, and the shortcut parallel for, to split work across multiple threads. In this episode, we will learn how to synchronise threads and how to avoid data inconsistencies caused by unsynchronised threads.
Synchronisation and race conditions
We’ve seen just how easy it is to write parallel code using OpenMP, but, now we need to make sure that the code we’re writing is both efficient and correct. To do that, we need some additional knowledge about thread synchronisation and race conditions. In the context of parallel computing, thread or rank (in the case of MPI) synchronisation plays a crucial role in guaranteeing the correctness of our program, particularly in regard to data consistency and integrity.
What is code correctness?
Code correctness in parallel programming is the guarantee that a program operates as expected in multi-threaded and multi-process environments, providing both consistent and valid results. This is usually about how a parallel algorithm deals with data accesses and modification, minimizing the occurrence of data inconsistencies creeping in.
So what is thread synchronisation? Thread synchronisation is the coordination of threads, which is usually done to avoid conflicts caused by multiple threads accessing the same piece of shared data. It’s important to synchronise threads properly so they are able to work together, and not interfere with data another thread is accessing or modifying. Synchronisation is also important for data dependency, to make sure that a thread has access to the data it requires. This is particularly important for algorithms which are iterative.
The synchronisation mechanisms in OpenMP are incredibly important tools, as they are used to avoid race conditions. Race conditions are have to be avoided, otherwise they can result in data inconsistencies if we have any in our program. A race condition happens when two, or more, threads access and modify the same piece of data at the same time. To illustrate this, consider the diagram below:
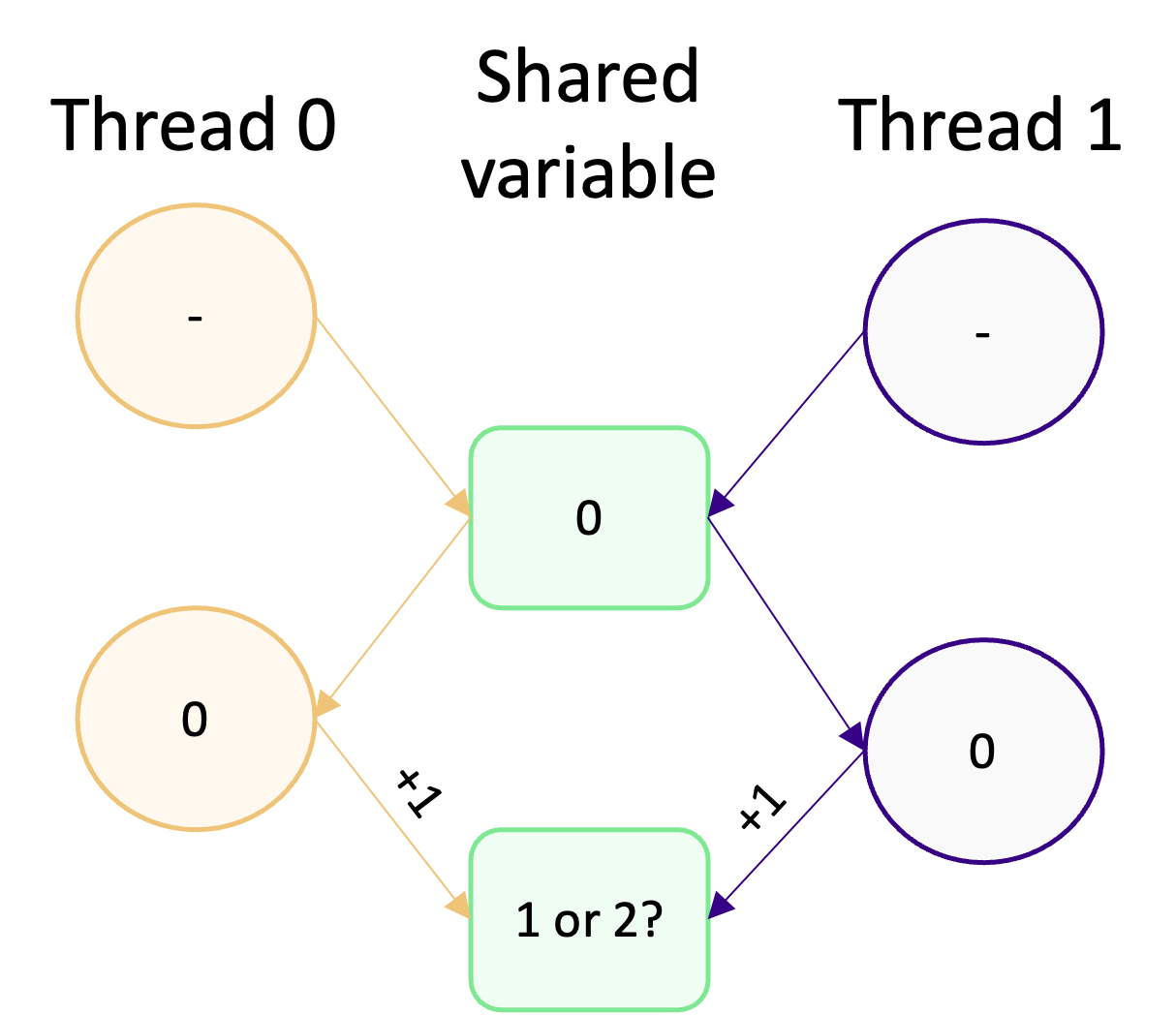
Two threads access the same shared variable (with the value 0) and increment it by 1. Intuitively, we might except the final value of the shared variable to be 2. However, due to the potential for concurrent access and modification, we can’t actually guarantee what it will be. If both threads access and modify the variable concurrently, then the final value will be 1. That’s because both variables read the initial value of 0, increment it by 1, and write to the shared variable.
In this case, it doesn’t matter if the variable update does or doesn’t happen concurrently. The inconsistency stems from the value initially read by each thread. If, on the other hand, one thread manages to access and modify the variable before the other thread can read its value, then we’ll get the value we expect (2). For example, if thead 0 increments the variable before thread 1 reads it, then thread 1 will read a value of 1 and increment that by 1 givusing us the correct value of 2. This illustrates why it’s called a race condition, because threads race each other to access and modify variables before another thread can!
Analogy: Editing a document
Imagine two people trying to update the same document at the same time. If they don’t communicate what they’re doing, they might edit the same part of the document and overwrite each others changes, ending up with a messy and inconsistent document (e.g. when they come to merge changes later). This is just like what happens with a race condition in OpenMP. Different threads accessing and modifying the same part of memory, which results in messy and inconsistent memory operations and probably an incorrect result.
Identifying race conditions
Take a look at the following code example. What’s the output when you compile and run this program? Where do you think the race condition is?
#include <omp.h> #include <stdio.h> #include <stdlib.h> #define NUM_TIMES 10000 int main(void) { int value = 0; #pragma omp parallel for for (int i = 0; i < NUM_TIMES; ++i) { value += 1; } printf("The final value is: %d\n", value); return EXIT_SUCCESS; }Solution
What you will notice is that when you run the program, the final value changes each time. The correct final value is 10,000 but you will often get a value that is lower than this. This is caused by a race condition, as explained in the previous diagram where threads are incrementing the value of
valuebefore another thread has finished with it.So the race condition is in the parallel loop and happens because of threads reading the value of
valuebefore it has been updated by other threads.
Synchronisation mechanisms
Synchronisation in OpenMP is all about coordinating the execution of threads, especially when there is data dependency in your program or when uncoordinated data access will result in a race condition. The synchronisation mechanisms in OpenMP allow us to control the order of access to shared data, coordinate data dependencies (e.g. waiting for calculations to be complete) and tasks (if one task needs to be done before other tasks can continue), and to potentially limit access to tasks or data to certain threads.
Barriers
Barriers are a the most basic synchronisation mechanism. They are used to create a waiting point in our program. When a
thread reaches a barrier, it waits until all other threads have reached the same barrier before continuing. To add a
barrier, we use the #pragma omp barrier directive. In the example below, we have used a barrier to synchronise threads
such that they don’t start the main calculation of the program until a look up table has been initialised (in parallel),
as the calculation depends on this data.
#pragma omp parallel
{
int thread_id = omp_get_num_thread();
/* The initialisation of the look up table is done in parallel */
initialise_lookup_table(thread_id);
#pragma omp barrier /* As all threads depend on the table, we have to wait until all threads
are done and have reached the barrier */
do_main_calculation(thread_id);
}
We can also put a barrier into a parallel for loop. In the next example, a barrier is used to ensure that the
calculation for new_matrix is done before it is copied into old_matrix.
double old_matrix[NX][NY];
double new_matrix[NX][NY];
#pragma omp parallel for
for (int i = 0; i < NUM_ITERATIONS; ++i) {
int thread_id = omp_get_thread_num();
iterate_matrix_solution(old_matrix, new_matrix, thread_id);
#pragma omp barrier /* You may want to wait until new_matrix has been updated by all threads */
copy_matrix(new_matrix, old_matrix);
}
Barriers introduce additional overhead into our parallel algorithms, as some threads will be idle whilst waiting for other threads to catch up. There is no way around this synchronisation overhead, so we need to be careful not to overuse barriers or have an uneven amount of work between threads. This overhead increases with the number of threads in use, and becomes even worse when the workload is uneven killing the parallel scalability.
Blocking thread execution and
nowaitMost parallel constructs in OpenMP will synchronise threads before they exit the parallel region. For example, consider a parallel for loop. If one thread finishes its work before the others, it doesn’t leave the parallel region and start on its next bit of code. It’s forced to wait around for the other threads to finish, because OpenMP forces threads to be synchronised.
This isn’t ideal if the next bit of work is independent of the previous work just finished. To avoid any wasted CPU time due to waiting around due to synchronisation, we can use the
nowaitclause which overrides the synchronisation that occurs and allow a “finished” thread to continue to its next chunk of work. In the example below, anowaitclause is used with a parallel for.#pragma omp parallel { #pragma omp for nowait /* with nowait the loop executes as normal, but... */ for (int i = 0; i < NUM_ITERATIONS; ++i) { parallel_function(); } /* ...if a thread finishes its work in the loop, then it can move on immediately to this function without waiting for the other threads to finish */ next_function(); }
Synchronisation regions
A common challenge in shared memory programming is coordinating threads to prevent multiple threads from concurrently modifying the same piece of data. One mechanism in OpenMP to coordinate thread access are synchronisation regions, which are used to prevent multiple threads from executing the same piece of code at the same time. When a thread reaches one of these regions, they queue up and wait their turn to access the data and execute the code within the region. The table below shows the types of synchronisation region in OpenMP.
| Region | Description | Directive |
|---|---|---|
| critical | Only one thread is allowed in the critical region. Threads have to queue up to take their turn. When one thread is finished in the critical region, it proceeds to execute the next chunk of code (not in the critical region) immediately without having to wait for other threads to finish. | #pragma omp critical |
| single | Single regions are used for code which needs to be executed only by a single thread, such as for I/O operations. The first thread to reach the region will execute the code, whilst the other threads will behave as if they’ve reached a barrier until the executing thread is finished. | #pragma omp single |
| master | A master region is identical to the single region other than that execution is done by the designated master thread (usually thread 0). | #pragma omp master |
The next example builds on the previous example which included a lookup table. In the the modified code, the lookup table is written to disk after it has been initialised. This happens in a single region, as only one thread needs to write the result to disk.
#pragma omp parallel
{
int thread_id = omp_get_num_thread();
initialise_lookup_table(thread_id);
#pragma omp barrier /* Add a barrier to ensure the lookup table is ready to be written to disk */
#pragma omp single /* We don't want multiple threads trying to write to file -- this could also be master */
{
write_table_to_disk();
}
do_main_calculation(thread_id);
}
If we wanted to sum up something in parallel (e.g. a reduction operation), we need to use a critical region to prevent a race condition when a threads is updating the reduction variable. For example, the code used in a previous exercise to demonstrate a race condition can be fixed as such,
int value = 0;
#pragma omp parallel for
for (int i = 0; i < NUM_TIMES; ++i) {
#pragma omp critical /* Now only one thread can read and modify `value` */
{
value += 1;
}
}
As we’ve added the critical region, only one thread can access and increment value at one time. This prevents the race
condition from earlier, because multiple threads no longer are able to read (and modify) the same variable before
other threads have finished with it. However in reality we shouldn’t write a reduction like this, but would use the
reduction
clause in the
parallel for directive, e.g. #pragma omp parallel for reduction(+:value)
Reporting progress
Create a program that updates a shared counter to track the progress of a parallel loop. Think about which type of synchronisation region you can use. Can you think of any potential problems with your implementation, what happens when you use different loop schedulers? You can use the code example below as your starting point.
NB: to compile this you’ll need to add
-lmto inform the linker to link to themathC library, e.g.gcc counter.c -o counter -fopenmp -lm#include <math.h> #include <omp.h> #define NUM_ELEMENTS 10000 int main(int argc, char **argv) { int array[NUM_ELEMENTS] = {0}; #pragma omp parallel for schedule(static) for (int i = 0; i < NUM_ELEMENTS; ++i) { array[i] = log(i) * cos(3.142 * i); } return 0; }Solution
To implement a progress bar, we have created two new variables:
progressandoutput_frequency. We useprogressto track the number of iterations completed across all threads. To prevent a race condition, we increment progress in a critical region. In the same critical region, we print the progress report out to screen wheneverprogressis divisible byoutput_frequency.#include <math.h> #include <omp.h> #include <stdio.h> #define NUM_ELEMENTS 1000 int main(int argc, char **argv) { int array[NUM_ELEMENTS] = {0}; int progress = 0; int output_frequency = NUM_ELEMENTS / 10; /* output every 10% */ #pragma omp parallel for schedule(static) for (int i = 0; i < NUM_ELEMENTS; ++i) { array[i] = log(i) * cos(3.142 * i); #pragma omp critical { progress++; if (progress % output_frequency == 0) { int thread_id = omp_get_thread_num(); printf("Thread %d: overall progress %3.0f%%\n", thread_id, (double)progress / NUM_ELEMENTS * 100.0); } } } return 0; }One problem with this implementation is that tracking progress like this introduces a synchronisation overhead at the end of each iteration, because of the critical region. In small loops like this, there’s usually no reason to track progress as the synchronisation overheads could be more significant than the time required to calculate each array element!
Preventing race conditions
A large amount of the time spent writing a parallel OpenMP application is usually spent preventing race conditions, rather than on the parallelisation itself. Earlier in the episode, we looked at critical regions as a way to synchronise threads and explored how be used to prevent race conditions in the previous exercise. In the rest of this section, we will look at the other mechanisms which can prevent race conditions, namely by setting locks or by using atomic operations.
Locks
Critical regions provide a convenient and straightforward way to synchronise threads and guard data access to prevent race conditions. But in some cases, critical regions may not be flexible or granular enough and lead to an excessive amount of serialisation. If this is the case, we can use locks instead to achieve the same effect as a critical region. Locks are a mechanism in OpenMP which, just like a critical regions, create regions in our code which only one thread can be in at one time. The main advantage of locks, over a critical region, is that we can be far more flexible with locks to protect different sized or fragmented regions of code, giving us more granular control over thread synchronisation. Locks are also far more flexible when it comes to making our code more modular, as it is possible to nest locks, or for accessing and modifying global variables.
In comparison to critical regions, however, locks are more complicated and difficult to use. Instead of using a single
#pragma, we have to initialise and free resources used for the locks, as well as set and unset where locks are in
effect. If we make a mistake and forget to unset a lock, then we lose all of the parallelism and could potentially
create a deadlock!
To create a lock and delete a lock, we use omp_init_lock() and omp_destroy_lock() respectively.
omp_lock_t lock; /* Locks are tracked via a lock variable, sometimes you'll create
a lock for large regions of code or sometimes locks for individual
variable updates */
omp_init_lock(&lock); /* Allocate resources for a lock using omp_init_lock */
/* The rest of our parallel algorithm goes here */
omp_destroy_lock(&lock); /* Deallocate resources for a lock */
To set and unset a lock, we use the omp_set_lock() and omp_unset_lock() functions.
omp_set_lock(&lock); /* When a thread reaches this function, it will only return from it when it can progress
into the lock region */
shared_variable += 1;
omp_unset_lock(&lock); /* By unsetting a lock, we signal that the next thread can start */
All together, using a lock should look something like in the example below.
#include <omp.h>
omp_lock_t lock; /* In practise, you should use a better name for your lock */
omp_init_lock(&lock); /* Allocate resources for the lock, before the parallel region */
int shared_variable = 0;
#pragma omp parallel
{
omp_set_lock(&lock); /* Set the lock, so only one thread can update shared_variable at once */
shared_variable += 1;
omp_unset_lock(&lock); /* Remember to unset the lock, to signal the next thread can enter the lock region */
}
omp_destroy_lock(&lock); /* Deallocate lock resources */
To recap, the main advantage of locks are increased flexibility and granularity for preventing race conditions. But the main disadvantage is the additional code complexity and the potential for deadlocks and poor parallel performance if we forget to or unset a lock in the wrong place.
Atomic operations
Another mechanism are atomic operations. In computing, an atomic operation is an operation which is performed without interrupted, meaning that one initiated, they are guaranteed to execute without interference from other operations. In OpenMP, this means atomic operations are operations which are done without interference from other threads. If we make modifying some value in an array atomic, then it’s guaranteed, by the compiler, that no other thread can read or modify that array until the atomic operation is finished. You can think of it as a thread having, temporary, exclusive access to something in our program. Sort of like a “one at a time” rule for accessing and modifying parts of the program.
To do an atomic operation, we use the omp atomic pragma before the operation we want to make atomic.
int shared_variable = 0;
int shared_array[4] = {0, 0, 0, 0};
/* Put the pragma before the shared variable */
#pragma omp parallel
{
#pragma omp atomic
shared_variable += 1;
}
/* Can also use in a parallel for */
#pragma omp parallel for
for (int i = 0; i < 4; ++i) {
#pragma omp atomic
shared_array[i] += 1;
}
Atomic operations are for single line operations or piece of code. As in the example above, we can do an atomic operation when we are updating variable but we can also do other things such as atomic assignment. Atomic operations are often less expensive than critical regions or locks, so they should be preferred when they can be used. However, it’s still important to not be over-zealous with using atomic operations as they can still introduce synchronisation overheads which can damage the parallel performance.
When should I prefer to use a critical region? Or an atomic operation, or a lock?
There are three mechanisms we can use to prevent race conditions: critical regions, locks and atomic operations. The question then is, when should I use which mechanism? The choice between what to use depends mainly on the specific requirements of your algorithm, and also a bit through trial and error.
Critical regions and locks are more appropriate when:
- You have some complex code which needs thread synchronisation, possible with a high level of granularity.
- When there is high contention, such as when multiple threads will frequently be accessing the same shared data.
- There is some degree of error handling or more advanced synchronisation patterns.
Atomic operations are good when:
- The operation which needs synchronisation is simple, such as needing to protect a single variable update in the parallel algorithm.
- There is low contention for shared data.
- When you need to be as performant as possible, as atomic operations generally have the lowest performance cost.
When comparing critical regions and locks, it is often better to use a critical region instead of a lock due to the simplicity of using a critical region.
Remove the race condition
In the following program, an array of values is created and then summed together using a parallel for loop.
#include <math.h> #include <omp.h> #include <stdio.h> #define ARRAY_SIZE 524288 int main(int argc, char **argv) { float sum = 0; float array[ARRAY_SIZE]; omp_set_num_threads(4); #pragma omp parallel for schedule(static) for (int i = 0; i < ARRAY_SIZE; ++i) { array[i] = cos(M_PI * i); } #pragma omp parallel for schedule(static) for (int i = 0; i < ARRAY_SIZE; i++) { sum += array[i]; } printf("Sum: %f\n", sum); return 0; }When we run the program multiple times, we expect the output
sumto have the value of0.000000. However, due to an existing race condition, the program can sometimes produce wrong output in different runs, as shown below:1. Sum: 1.000000 2. Sum: -1.000000 3. Sum: 2.000000 4. Sum: 0.000000 5. Sum: 2.000000Find and fix the race condition in the program. Try using both an atomic operation and by using locks.
Solution
We only need to modify the second loop, as each iteration in the first loop is working on an independent piece of memory, meaning there will be no race condition. In the code below, we have used an atomic operation to increment
sum.#include <math.h> #include <omp.h> #include <stdio.h> #define ARRAY_SIZE 524288 int main(int argc, char **argv) { float sum = 0; float array[ARRAY_SIZE]; omp_set_num_threads(4); #pragma omp parallel for schedule(static) for (int i = 0; i < ARRAY_SIZE; ++i) { array[i] = cos(M_PI * i); } #pragma omp parallel for schedule(static) for (int i = 0; i < ARRAY_SIZE; i++) { #pragma omp atomic sum += array[i]; } printf("Sum: %f\n", sum); return 0; }Using a critical region or a lock would also work here. If the loop was more complicated than a single increment operation, then we would have to use a critical region or a lock. You can see the solution using a lock here. If you have to spare time, you can play around with “forgetting” to unset a lock to see what happens.
Of course in reality, we wouldn’t bother doing this to the second loop. We’d just use a parallel reduction instead to handle thread synchronisation for us!
#pragma omp parallel for schedule(static) reduction(+:sum) for (int i = 0; i < ARRAY_SIZE; ++i) { sum += array[i]; }
Key Points
Synchronising threads is important to ensure data consistency and code correctness
A race condition happens when multiple threads try to access and modify the same piece of data at the same time
OpenMP has many synchronisation mechanisms which are used to coordinate threads
Atomic operations, locks and critical regions can be used to prevent race conditions
Introduction to Hybrid Parallelism
Overview
Teaching: 20 min
Exercises: 20 minQuestions
What is hybrid parallelism?
How could hybrid parallelism benefit my software?
Objectives
Learn what hybrid parallelism is
Understand the advantages of disadvantages of hybrid parallelism
Learn how to use OpenMP and MPI together
At this point in the lesson, we’ve introduced the basics you need to get out there and start writing parallel code using OpenMP. There is one thing still worth being brought to your attention, and that is hybrid parallelism.
The Message Passing Interface (MPI)
In this episode, we will assume you have some knowledge about the Message Passing Interface (MPI) and that you have a basic understand of how to paralleise code using MPI. If you’re not sure, you can think of MPI as being like an OpenMP program where everything is in a
pragma omp paralleldirective.
What is hybrid parallelism?
When we talk about hybrid paralleism, what we’re really talking about is writing parallel code using more than one parallelisation paradigm. The reason we want to do this is to take advantage of the strengths of each paradigm to improve the performance, scaling and efficiency of our parallel core. The most common form of hybrid parallelism in research is MPI+X. What this means is that an application is mostly parallelised using the Message Passing Interface (MPI), which has been extended using some +X other paradigm. A common +X is OpenMP, creating MPI+OpenMP.
Heterogeneous Computing
An MPI+OpenMP scheme is known as homogenous computing, meaning all the processing units involved are of the same type. The opposite is heterogeneous computing, where different types of processing architectures are used such as CPUs, GPUs (graphics processing units), TPUs (tensor processing units) and FGPAs (field-programmable gate arrays). The goal of heterogeneous computing is to leverage the strengths of each processor type to achieve maximum performance and efficiency. The most common in research will be CPU and GPU.
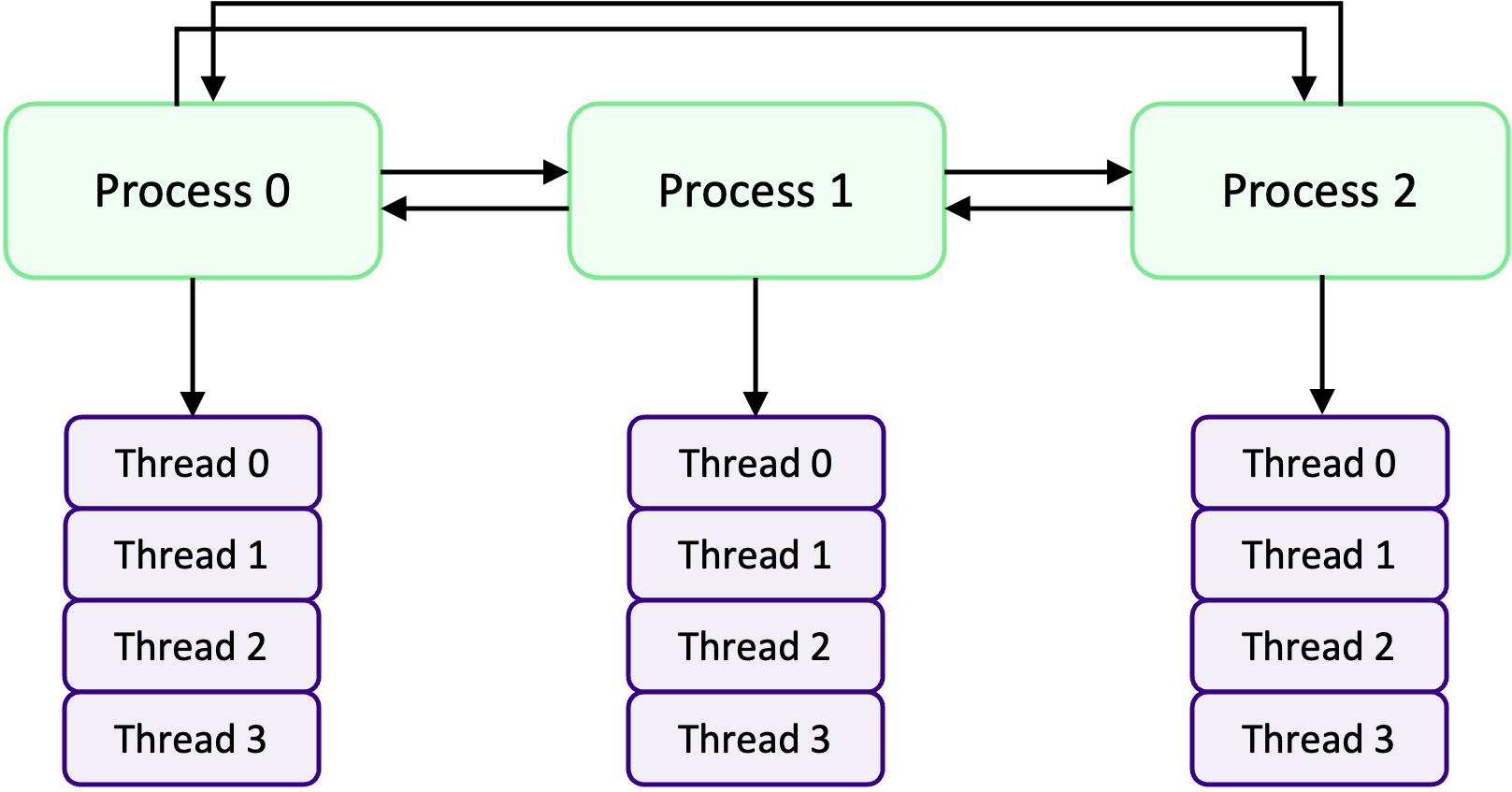
In an MPI+OpenMP application, one or multiple MPI processes/ranks are created each of which spawn their own set of OpenMP threads as shown in the diagram above. The key thing to realise is that by combining MPI and OpenMP, we can scale an OpenMP program from only being able to use the resources on a single HPC compute node to being able to use multiple compute nodes. We can think of it was MPI being in charge of parallelising a program across nodes, whilst OpenMP is responsible for the parallelism on a node.
The MPI processes are able to communicate data with one another and the threads within the same MPI process are still using shared-memory, so do not need to communicate data. However, threads in other MPI processes cannot use the data that threads in another MPI process have access to due to each MPI process having its own memory space. It is still possible to communicate thread-to-thread, but we have to be very careful and explicitly set up communication between specific threads using the parent MPI processes.
As an example of how resources could be split using an MPI+OpenMP approach, consider a HPC cluster with some number of compute nodes with each having 64 CPU cores. One approach would be to spawn one MPI process per rank which spawns 64 OpenMP threads, or 2 MPI processes which both spawn 32 OpenMP threads, and so on and so forth.
Advantages
Improved memory efficiency
Since MPI processes each have their own private memory space, there is almost aways some data replication. This could be on small pieces of data, such as some physical constants each MPI rank needs, or it could be large pieces of data such a grid of data or a large dataset. When there is large data being replicated in each rank, the memory requirements of an MPI program can rapidly increase making it unfeasible to run on some systems. In an OpenMP application, we don’t have to worry about this as the threads share the same memory space and so there is no need for data replication. A huge advantage of MPI+OpenMP is not having to replicate as much data, because there are less MPI ranks which require replicated data.
Improved scaling and load balancing
With MPI, we can scale our OpenMP applications and use resources on multiple nodes rather than being limited to only the resources on a single node. The advantage here is obvious. But by using OpenMP to handle the parallelism on a node, we can more easily control the work balance, in comparison to a pure MPI implementation at least, as we can use OpenMP’s schedulers to address imbalance on a node. There is typically also a reduction in communication overheads, as there is no communication required between threads (although this overhead may be replaced by thread synchronisation overheads) which can improve the performance of algorithms which previously required communication such as those which require exchanging data between overlapping sub-domains (halo exchange).
Disadvantages
More difficult to write and maintain
Writing correct and efficient parallel code in pure MPI and pure OpenMP is hard enough, so combining both of them is, naturally, even more difficult to write and maintain. Most of the difficulty comes from having to combine both parallelism models in an easy to read and maintainable fashion, as the interplay between the two parallelism models adds complexity to the code we write. We also have to ensure we do not introduce any race conditions, making sure to synchronise threads and ranks correctly and at the correct parts of the program. Finally, because we are using two parallelism models, MPI+OpenMP code bases are larger than a pure MPI or OpenMP version, making the overall maintainability more challenging.
Increased overheads
Most implementations of a hybrid scheme will be slower than a pure implementation. This derives from additional overheads, either from introducing MPI communication or from now having to worry about thread synchronisation. The combination of coordinating and synchronisation between MPI processes and OpenMP threads increases the overheads required to enable hybrid parallelism.
Limited portability
The portability for an MPI+OpenMP application is usually more limited, as there are more libraries and compiler versions to consider which have to be tested for compatibility. For example, we may need to account for compiler-specific directives for OpenMP and ensure that different MPI implementations and versions (as well as OpenMP) are compatible. Most of this can, however, be mitigated with good documentation and a robust build system.
When do I need to use hybrid parallelism?
So, when should we use a hybrid scheme? A hybrid scheme is particularly beneficial in scenarios where you need to leverage the strength of both the shared- and distributed-memory parallelism paradigms. MPI is used to exploit lots of resources across nodes on a HPC cluster, whilst OpenMP is used to efficiently (and somewhat easily) parallelise the work each MPI task is required to do.
The most common reason for using a hybrid scheme is for large-scale simulations, where the workload doesn’t fit or work efficiently in a pure MPI or OpenMP implementation. This could be because of memory constraints due to data replication, or due to poor/complex workload balance which are difficult to handle in MPI, or because of inefficient data access patterns from how ranks are coordinated. Of course, your mileage may vary and it is not always appropriate to use a hybrid scheme. It could be better to think about other ways or optimisations to decrease overheads and memory requirements, or to take a different approach to improve the work balance.
Writing a hybrid parallel application
To demonstrate how to use MPI+OpenMP, we are going to write a program which computes an approximation for $\pi$ using a Riemann sum. This is not a great example to extol the virtues of hybrid parallelism, as it is only a small problem. However, it is a simple problem which can be easily extended and parallelised. Specifically, we will write a program to solve to integral to compute the value of $\pi$,
[\int_{0}^{1} \frac{4}{1 + x^{2}} ~ \mathrm{d}x = 4 \tan^{-1}(x) = \pi]
There are a plethora of methods available to numerically evaluate this integral. To keep the problem simple, we will re-cast the integral into a easier-to-code summation. How we got here isn’t that important for our purposes, but what we will be implementing in code is the follow summation,
[\pi = \lim_{n \to \infty} \sum_{i = 0}^{n} \frac{1}{n} ~ \frac{4}{1 + x_{i}^{2}}]
where $x_{i}$ is the the midpoint of the $i$-th rectangle. To get an accurate approximation of $\pi$, we’ll need to split the domain into a large number of smaller rectangles.
A simple parallel implementation using OpenMP
To begin, let’s first write a serial implementation as in the code example below.
#include <stdio.h>
#include <time.h>
#include <unistd.h>
#define PI 3.141592653589793238462643
int main(void)
{
struct timespec begin;
clock_gettime(CLOCK_MONOTONIC_RAW, &begin);
/* Initialise parameters. N is the number of rectangles we will sum over,
and h is the width of each rectangle (1 / N) */
const long N = (long)1e10;
const double h = 1.0 / N;
double sum = 0.0;
/* Compute the summation. At each iteration, we calculate the position x_i
and use this value in 4 / (1 + x * x). We are not including the 1 / n
factor, as we can multiply it once at the end to the final sum */
for (long i = 0; i <= N; ++i) {
const double x = h * (double)i;
sum += 4.0 / (1.0 + x * x);
}
/* To attain our final value of pi, we multiply by h as we did not include
this in the loop */
const double pi = h * sum;
struct timespec end;
clock_gettime(CLOCK_MONOTONIC_RAW, &end);
printf("Calculated pi %18.6f error %18.6f\n", pi, pi - PI);
printf("Total time = %f seconds\n", (end.tv_nsec - begin.tv_nsec) / 1000000000.0 + (end.tv_sec - begin.tv_sec));
return 0;
}
In the above, we are using $N = 10^{10}$ rectangles (using this number of rectangles is overkill, but is used to
demonstrate the performance increases from parallelisation. If we save this (as pi.c), compile and run we should get
output as below,
$ gcc pi.c -o pi.exe
$ ./pi.exe
Calculated pi 3.141593 error 0.000000
Total time = 34.826832 seconds
You should see that we’ve compute an accurate approximation of $\pi$, but it also took a very long time at 35 seconds! To speed this up, let’s first parallelise this using OpenMP. All we need to do, for this simple application, is to use a parallel for to split the loop between OpenMP threads as shown below.
/* Parallelise the loop using a parallel for directive. We will set the sum
variable to be a reduction variable. As it is marked explicitly as a reduction
variable, we don't need to worry about any race conditions corrupting the
final value of sum */
#pragma omp parallel for shared(N, h), reduction(+:sum)
for (long i = 0; i <= N; ++i) {
const double x = h * (double)i;
sum += 4.0 / (1.0 + x * x);
}
/* For diagnostics purposes, we are also going to print out the number of
threads which were spawned by OpenMP */
printf("Calculated using %d OMP threads\n", omp_get_max_threads());
Once we have made these changes (you can find the completed implementation here), compiled and run the program, we can see there is a big improvement to the performance of our program. It takes just 5 seconds to complete, instead of 35 seconds, to get our approximate value of $\pi$, e.g.:
$ gcc -fopenmp pi-omp.c -o pi.exe
$ ./pi.exe
Calculated using 8 OMP threads
Calculated pi 3.141593 error 0.000000
Total time = 5.166490 seconds
A hybrid implementation using MPI and OpenMP
Now that we have a working parallel implementation using OpenMP, we can now expand our code to a hybrid parallel code by implementing MPI. In this example, we can porting an OpenMP code to a hybrid MPI+OpenMP application but we could have also done this the other way around by porting an MPI code into a hybrid application. Neither “evolution” is more common or better than the other, the route each code takes toward becoming hybrid is different.
So, how do we split work using a hybrid approach? One approach for an embarrassingly parallel problem, such as the one we’re working on is to can split the problem size into smaller chunks across MPI ranks, and to use OpenMP to parallelise the work. For example, consider a problem where we have to do a calculation for 1,000,000 input parameters. If we have four MPI ranks each of which will spawn 10 threads, we could split the work evenly between MPI ranks so each rank will deal with 250,000 input parameters. We will then use OpenMP threads to do the calculations in parallel. If we use a sequential scheduler, then each thread will do 25,000 calculations. Or we could use OpenMP’s dynamic scheduler to automatically balance the workload. We have implemented this situation in the code example below.
/* We have an array of input parameters. The calculation which uses these parameters
is expensive, so we want to split them across MPI ranks */
struct input_par_t input_parameters[total_work];
/* We need to determine how many input parameters each rank will process (we are
assuming total_work is cleanly divisible) and also lower and upper indices of
the input_parameters array the rank will work on */
int work_per_rank = total_work / num_ranks;
int rank_lower_limit = my_rank * work_per_rank;
int rank_upper_limit = (my_rank + 1) * work_per_rank;
/* The MPI rank now knows which subset of data it will work on, but we will use
OpenMP to spawn threads to execute the calculations in parallel. We'll make sure
of the auto scheduler to best determine how to balance the work */
#pragma omp parallel for schedule(auto)
for (int i = rank_lower_limit; i < rank_upper_limit; ++i) {
some_expensive_calculation(input_parameters[i]);
}
Still not sure about MPI?
If you’re still a bit unsure of how MPI is working, you can basically think of it as wrapping large parts of your code in a
pragma omp parallelregion as we saw in an earlier episode. We can re-write the code example above in the same way, but using OpenMP thread IDs instead.struct input_par_t input_parameters[total_work]; #pragma omp parallel { int num_threads = omp_get_num_threads(); int thread_id = omp_get_thread_num(); int work_per_thread = total_work / num_threads; int thread_lower = thread_id * work_per_thread; int thread_upper = (thread_id + 1) * work_per_thread; for(int i = thread_lower; i < thread_upper; ++i) { some_expensive_calculation(input_parameters[i]); } }
In the above example, we have only included the parallel region of code. It is unfortunately not as simple as this, because we have to deal with the additional complexity from using MPI. We need to initialise MPI, as well as communicate and receive data and deal with the other complications which come with MPI. When we include all of this, our code example becomes much more complicated than before. In the next code block, we have implemented a hybrid MPI+OpenMP approximation of $\pi$ using the same Riemann sum method.
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <unistd.h>
#include <mpi.h>
#include <omp.h>
#define PI 3.141592653589793238462643
#define ROOT_RANK 0
int main(void)
{
struct timespec begin;
clock_gettime(CLOCK_MONOTONIC_RAW, &begin);
/* We have to initialise MPI first and determine the number of ranks and
which rank we are to be able to split work with MPI */
int my_rank;
int num_ranks;
MPI_Init(NULL, NULL);
MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
MPI_Comm_size(MPI_COMM_WORLD, &num_ranks);
/* We can leave this part unchanged, the parameters per rank will be the
same */
double sum = 0.0;
const long N = (long)1e10;
const double h = 1.0 / N;
/* The OpenMP parallelisation is almost the same, we are still using a
parallel for to do the loop in parallel. To parallelise using MPI, we
have each MPI rank do every num_rank-th iteration of the loop. Each rank
will do N / num_rank iterations split between it's own OpenMP threads */
#pragma omp parallel for shared(N, h, my_rank, num_ranks), reduction(+:sum)
for (long i = my_rank; i <= N; i = i + num_ranks) {
const double x = h * (double)i;
sum += 4.0 / (1.0 + x * x);
}
/* The sum we compute is per rank now, but only includes N / num_rank
elements so is not the final value of pi */
const double rank_pi = h * sum;
/* To get the final value, we will use a reduction across ranks to sum up
the contributions from each MPI rank */
double reduced_pi;
MPI_Reduce(&rank_pi, &reduced_pi, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
if (my_rank == ROOT_RANK) {
struct timespec end;
clock_gettime(CLOCK_MONOTONIC_RAW, &end);
/* Let's check how many ranks are running and how many threads each rank
is spawning */
printf("Calculated using %d MPI ranks each spawning %d OMP threads\n", num_ranks, omp_get_max_threads());
printf("Calculated pi %18.6f error %18.6f\n", reduced_pi, reduced_pi - PI);
printf("Total time = %f seconds\n", (end.tv_nsec - begin.tv_nsec) / 1000000000.0 + (end.tv_sec - begin.tv_sec));
}
MPI_Finalize();
return 0;
}
So you can see that it’s much longer and more complicated; although not much more than a pure MPI
implementation. To compile our hybrid program, we use the MPI compiler command mpicc with
the argument -fopenmp. We can then either run our compiled program using mpirun.
$ mpicc -fopenmp 05-pi-omp-mpi.c -o pi.exe
$ mpirun pi.exe
Calculated 8 MPI ranks each spawning 8 OMP threads
Calculated pi 3.141593 error 0.000000
Total time = 5.818889 seconds
Ouch, this took longer to run than the pure OpenMP implementation (although only marginally longer in this example!). You may have noticed that we have 8 MPI ranks, each of which are spawning 8 of their own OpenMP threads. This is an important thing to realise. When you specify the number of threads for OpenMP to use, this is the number of threads each MPI process will spawn. So why did it take longer? With each of the 8 MPI ranks spawning 8 threads, 64 threads threads were in flight. More threads means more overheads and if, for instance, we have 8 CPU Cores, then contention arises as each thread competes for access to a CPU core.
Let’s improve this situation by using a combination of rank and threads so that $N_{\mathrm{ranks}} N_{\mathrm{threads}}
\le 8$. One way to do this is by setting the OMP_NUM_THREADS environment variable and by specifying the number of
processes we want to spawn with mpirun. For example, we can spawn two MPI processes which will both spawn 4 threads
each.
$ export OMP_NUM_THREADS 4
$ mpirun -n 2 pi.exe
Calculated using 4 OMP threads and 2 MPI ranks
Calculated pi 3.141593 error 0.000000
Total time = 5.078829 seconds
This is better now, as threads aren’t fighting for access to a CPU core. If we change the number of ranks to 1 and the number of threads to 8, will it take the same amount of time to run as the pure OpenMP implementation?
$ export OMP_NUM_THREADS 8
$ mpirun -n 1 pi.exe
Calculated using 8 OMP threads and 1 MPI ranks
Calculated pi 3.141593 error 0.000000
Total time = 5.328421 seconds
In this case, we don’t. It takes slightly longer to run because of the overhead associated with MPI. Even when we use one MPI rank, we still have to initialise MPI, set the rank number, and so on. All of this takes time. The same happens with using 8 ranks and 1 thread per rank, as there is still a slight overhead related to scheduling the work for that single OpenMP thread.
$ export OMP_NUM_THREADS 1
$ mpirun -n 8 pi.exe
Calculated using 1 OMP threads and 8 MPI ranks
Calculated pi 3.141593 error 0.000000
Total time = 5.377609 seconds
How many ranks and threads should I use?
How many ranks and threads you should use depends on lots of parameters, such as the size of your problem (e.g. do you need a large number of threads but a smaller number of ranks to improve memory efficiency?), the hardware you are using and the design/structure of your code. It’s unfortunately very difficult to predict the best combination of ranks and threads. Often we won’t know until after we’ve run lots of tests and gained some intuition. It’s a delicate balance of balancing overheads associated with thread synchronisation in OpenMP and data communication in MPI. As mentioned earlier, a hybrid implementation will typically be slower than a “pure” MPI implementation for example.
Optimum combination of threads and ranks for approximating $\pi$
Try various combinations of the number of OpenMP threads and number of MPI processes. For this program, what’s faster? Only using MPI, only using OpenMP or a hybrid implementation? Why do you think this is the fastest method of parallelisation?
Note that there will be some level of variance in the run time each time you run the program, due to factors such as other programs using your CPU at the same time. You should run each thread/rank combination multiple time to get an average.
Solution
There is not really a right answer here, as the best combination will depend on lots of factors such as the hardware you are running the program on. On a MacBook Pro with a 6-core M1 Pro, the best combination of ranks and threads was, rather naturally, when either $N_{\mathrm{ranks}} = 1$, $N_{\mathrm{threads}} = 6$ and $N_{\mathrm{ranks}} = 6$, $N_{\mathrm{threads}} = 1$ with the former being slightly faster. Otherwise, we found the best balance was $N_{\mathrm{ranks}} = 2$, $N_{\mathrm{threads}} = 3$.
Submitting a hybrid application to Slurm
There isn’t that much you have to do different when it comes to submitting a MPI+OpenMP application to Slurm. In addition to the standard parameters for controlling the length of the job, the resources it requires and etc., we also need to set additional parameters to tell Slurm how to distribute the threads and ranks across the hardware available. For example, instead of only settings the number of ranks, we need to set the number of tasks (or MPI ranks) and how many CPUs to assign to each task:
#!/bin/bash
#SBATCH --time=00:05:00 # Walltime limit for job
#SBATCH --nodes=2 # Number of nodes to use
#SBATCH --tasks-per-node=2 # Number of MPI ranks/tasks to create
#SBATCH --cpus-per-task=20 # Number of CPUs available to each MPI rank/task
#SBATCH --partition=standard # Partition/queue name
# Export the number of threads as cpus-per-task
export OMP_NUM_THREADS=$SLURM_CPUS_PER_TASK
# Use srun to run the program (but could also use mpirun/mpiexec)
srun ./pi.exe
Which thread goes where?
It’s not necessarily always clear how threads and ranks will be distributed across cores, and you can accidentally overlap or oversubscribe CPU cores rather easily! An excellent tool for seeing how threads and ranks get distributed is a program called xthi.
In this exercise, we will use
xthito experiment with how OpenMP threads and MPI ranks are distributed across the CPU cores. The first thing to do is download and compilexthionto your HPC system. Then using this slurm script as your starting point, experiment with changing the number of tasks per node and cpus per node and seeing how threads and ranks are distributed.#!/bin/bash #SBATCH --time=00:01:00 #SBATCH --nodes=1 #SBATCH --ntasks=4 #SBATCH --tasks-per-node=2 #SBATCH --cpus-per-task=2 #SBATCH --partition=YOUR_PARTITION export OMP_NUM_THREADS=$SLURM_CPUS_PER_TASK mpirun -np $SLURM_NTASKS xthi
Key Points
Hybrid parallelism is the combination of two or more different parallelisation schemes
One of the most forms of hybrid parallelism is to use MPI with OpenMP
The main advantages of a hybrid MPI+OpenMP approach are reduced memory usage and improved scaling and load balancing
However, this comes at the cost of increased overheads, code complexity and potentially limited portability
In MPI+OpenMP, a common approach is to split up jobs across MPI processes and to parallelise job execution using OpenMP
Survey
Overview
Teaching: min
Exercises: minQuestions
Objectives
Key Points