Collective Communication
Overview
Teaching: 0 min
Exercises: 0 minQuestions
How do I get data to more than one rank?
Objectives
Describe what is meant by collective communication, and its advantages
Describe how to synchronise ranks using MPI
Broadcast a message to multiple ranks
Describe how to split and send data across multiple ranks, and receive data from multiple ranks
Describe how to “reduce” values from across multiple ranks
Describe how to perform broadcasting and reduction in a single MPI call
The previous episode showed how to send data from one rank to another using point-to-point communication. If we wanted to send data from multiple ranks to a single rank to, for example, add up the value of a variable across multiple ranks, we have to manually loop over each rank to communicate the data. This type of communication, where multiple ranks talk to one another known as called collective communication. In the code example below, point-to-point communication is used to calculate the sum of the rank numbers - feel free to try it out!
#include <stdio.h>
#include <mpi.h>
int main(int argc, char **argv) {
int my_rank, num_ranks;
// First call MPI_Init
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
MPI_Comm_size(MPI_COMM_WORLD, &num_ranks);
int sum;
MPI_Status status;
// Rank 0 is the "root" rank, where we'll receive data and sum it up
if (my_rank == 0) {
sum = my_rank;
// Start by receiving the rank number from every rank, other than itself
for (int i = 1; i < num_ranks; ++i) {
int recv_num;
MPI_Recv(&recv_num, 1, MPI_INT, i, 0, MPI_COMM_WORLD, &status);
sum += recv_num;
}
// Now sum has been calculated, send it back to every rank other than the root
for (int i = 1; i < num_ranks; ++i) {
MPI_Send(&sum, 1, MPI_INT, i, 0, MPI_COMM_WORLD);
}
} else { // All other ranks will send their rank number and receive sum */
MPI_Send(&my_rank, 1, MPI_INT, 0, 0, MPI_COMM_WORLD);
MPI_Recv(&sum, 1, MPI_INT, 0, 0, MPI_COMM_WORLD, &status);
}
printf("Rank %d has a sum of %d\n", my_rank, sum);
// Call finalize at the end
return MPI_Finalize();
}
For it’s use case, the code above works perfectly fine. However, it isn’t very efficient when you need to communicate large amounts of data, have lots of ranks, or when the workload is uneven (due to the blocking communication). It’s also a lot of code to not do very much, which makes it easy to introduce mistakes in our code. Another mistake in this example
would be to start the loop over ranks from 0, which would cause a deadlock! It’s actually quite a common mistake for new MPI users to write something like the above.
We don’t need to write code like this (unless we want complete control over the data communication), because MPI has access to collective communication functions to abstract all of this code for us. The above code can be replaced by a single collective communication function. Collection operations are also implemented far more efficiently in the MPI library than we could ever write using point-to-point communications.
There are several collective operations that are implemented in the MPI standard. The most commonly-used are:
| Type | Description |
|---|---|
| Synchronisation | Wait until all processes have reached the same point in the program. |
| One-To-All | One rank sends the same message to all other ranks. |
| All-to-One | All ranks send data to a single rank. |
| All-to-All | All ranks have data and all ranks receive data. |
Synchronisation
Barrier
The most simple form of collective communication is a barrier. Barriers are used to synchronise ranks by adding a point
in a program where ranks must wait until all ranks have reached the same point. A barrier is a collective operation
because all ranks need to communicate with one another to know when they can leave the barrier. To create a barrier, we
use the MPI_Barrier() function,
int MPI_Barrier(
MPI_Comm comm
);
comm: |
The communicator to add a barrier to |
When a rank reaches a barrier, it will pause and wait for all the other ranks to catch up and reach the barrier as well. As ranks waiting at a barrier aren’t doing anything, barriers should be used sparingly to avoid large synchronisation overheads, which affects the scalability of our program. We should also avoid using barriers in parts of our program has have complicated branches, as we may introduce a deadlock by having a barrier in only one branch.
In practise, there are not that many practical use cases for a barrier in an MPI application. In a shared-memory environment, synchronisation is important to ensure consistent and controlled access to shared data. But in MPI, where each rank has its own private memory space and often resources, it’s rare that we need to care about ranks becoming out-of-sync. However, one usecase is when multiple ranks need to write sequentially to the same file. The code example below shows how you may handle this by using a barrier.
for (int i = 0; i < num_ranks; ++i) {
if (i == my_rank) { /* One rank writes to the file */
write_to_file();
}
MPI_Barrier(MPI_COMM_WORLD); /* Wait for data to be written, so it is sequential and ordered */
}
One-To-All
Broadcast
We’ll often find that we need to data from one rank to all the other ranks. One approach, which is not very efficient,
is to use MPI_Send() in a loop to send the data from rank to rank one by one. A far more efficient approach is to use
the collective function MPI_Bcast() to broadcast the data from a root rank to every other rank. The MPI_Bcast()
function has the following arguments,
int MPI_Bcast(
void *data,
int count,
MPI_Datatype datatype,
int root,
MPI_Comm comm
);
data: |
The data to be sent to all ranks |
count: |
The number of elements of data |
datatype: |
The datatype of the data |
root: |
The rank which data will be sent from |
comm: |
The communicator containing the ranks to broadcast to |
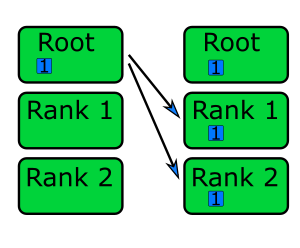
MPI_Bcast() is similar to the MPI_Send() function, but MPI_Bcast() sends
the data to all ranks (other than itself, where the data already is) instead of a single rank, as shown in the
diagram below.
There are lots of use cases for broadcasting data. One common case is when data is sent back to a “root” rank to process, which then broadcasts the results back out to all the other ranks. Another example, shown in the code exert below, is to read data in on the root rank and to broadcast it out. This is useful pattern on some systems where there are not enough resources (filesystem bandwidth, limited concurrent I/O operations) for every ranks to read the file at once.
int data_from_file[NUM_POINTS]
/* Read in data from file, and put it into data_from_file. We are only reading data
from the root rank (rank 0), as multiple ranks reading from the same file at the
same time can sometimes result in problems or be slower */
if (my_rank == 0) {
get_data_from_file(data_from_file);
}
/* Use MPI_Bcast to send the data to every other rank */
MPI_Bcast(data_from_file, NUM_POINTS, MPI_INT, 0, MPI_COMM_WORLD);
Sending greetings
Send a message from rank 0 saying “Hello from rank 0” to all ranks using
MPI_Bcast().Solution
#include <mpi.h> #include <stdio.h> #include <string.h> #define NUM_CHARS 32 int main(int argc, char **argv) { int my_rank, num_ranks; MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &my_rank); MPI_Comm_size(MPI_COMM_WORLD, &num_ranks); char message[NUM_CHARS]; if (my_rank == 0) { strcpy(message, "Hello from rank 0"); } MPI_Bcast(message, NUM_CHARS, MPI_CHAR, 0, MPI_COMM_WORLD); printf("I'm rank %d and I got the message '%s'\n", my_rank, message); return MPI_Finalize(); }
Scatter
One way to parallelise processing amount of data is to have ranks process a subset of the data. One method for
distributing the data to each rank is to have a root rank which prepares the data, and then send the data to every rank.
The communication could be done manually using point-to-point communication, but it’s easier, and faster, to use a
single collective communication. We can use MPI_Scatter() to split the data into equal sized chunks and communicate
a diferent chunk to each rank, as shown in the diagram below.
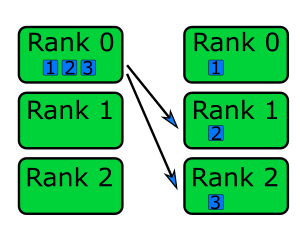
MPI_Scatter() has the following arguments,
int MPI_Scatter(
void *sendbuf,
int sendcount,
MPI_Datatype sendtype,
void *recvbuffer,
int recvcount,
MPI_Datatype recvtype,
int root,
MPI_Comm comm
);
*sendbuf: |
The data to be scattered across ranks (only important for the root rank) |
sendcount: |
The number of elements of data to send to each root rank (only important for the root rank) |
sendtype: |
The data type of the data being sent (only important for the root rank) |
*recvbuffer: |
A buffer to receive data into, including the root rank |
recvcount: |
Th number of elements of data to receive. Usually the same as sendcount |
recvtype: |
The data type of the data being received. Usually the same as sendtype |
root: |
The rank data is being scattered from |
comm: |
The communicator |
The data to be scattered is split into even chunks of size sendcount. If sendcount is 2 and sendtype is
MPI_INT, then each rank will receive two integers. The values for recvcount and recvtype are the same as
sendcount and sendtype. If the total amount of data is not evenly divisible by the number of processes,
MPI_Scatter() will not work. In this case, we need to use
MPI_Scatterv() instead to specify the amount of data each
rank will receive. The code example below shows MPI_Scatter() being used to send data which has been initialised only
on the root rank.
#define ROOT_RANK 0
int send_data[NUM_DATA_POINTS]
if (my_rank == ROOT_RANK) {
initialise_send_data(send_data); /* The data which we're going to scatter only needs to exist in the root rank */
}
/* Calculate the elements of data each rank will get, and allocate space for
the receive buffer -- we are assuming NUM_DATA_POINTS is divisible by num_ranks */
int num_per_rank = NUM_DATA_POINTS / num_ranks;
int *scattered_data_for_rank = malloc(num_per_rank * sizeof(int));
/* Using a single function call, the data has been split and communicated evenly between all ranks */
MPI_Scatter(send_data, num_per_rank, MPI_INT, scattered_data_for_rank, num_per_rank, MPI_INT, ROOT_RANK, MPI_COMM_WORLD);
All-To-One
Gather
The opposite of scattering from one rank to multiple, is to gather data from multiple ranks into a single rank. We can
do this by using the collection function MPI_Gather(), which has the arguments,
int MPI_Gather(
void *sendbuf,
int sendcount,
MPI_Datatype sendtype,
void *recvbuff,
int recvcount,
MPI_Datatype recvtype,
int root,
MPI_Comm comm
);
*sendbuff: |
The data to send to the root rank |
sendcount: |
The number of elements of data to send |
sendtype: |
The data type of the data being sent |
recvbuff: |
The buffer to put gathered data into (only important for the root rank) |
recvcount: |
The number of elements being received, usually the same as sendcount |
recvtype: |
The data type of the data being received, usually the same as sendtype |
root: |
The root rank, where data will be gathered to |
comm: |
The communicator |
The receive buffer needs to be large enough to hold data data from all of the ranks. For example, if there are 4 ranks
sending 10 integers, then recvbuffer needs to be able to store at least 40 integers. We can think of MPI_Gather()
as being the inverse of MPI_Scatter(). This is shown in the diagram below, where data from each rank on the left is
sent to the root rank (rank 0) on the right.
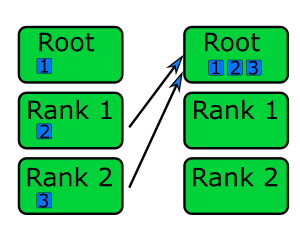
In the code example below, MPI_Gather() is used to gather the contents of rank_data from each rank, to rank 0 (the
root rank).
int rank_data[NUM_DATA_POINTS];
/* Each rank generates some data, including the root rank */
for (int i = 0; i < NUM_DATA_POINTS; ++i) {
rank_data[i] = (rank + 1) * (i + 1);
}
/* To gather all of the data, we need a buffer to store it. To make sure we have enough
space, we need to make sure we allocate enough memory on the root rank */
int recv_count = NUM_DATA_POINTS * num_ranks;
int *gathered_data = malloc(recv_count * sizeof(int));
/* MPI_Gather is used in a similar way to MPI_Scatter. Note how that even though we have
allocated recv_count elements for *gathered_data, MPI_Gather has recv_count set to
NUM_DATA_POINTS. This is because we are expecting to receive that many elements from
each rank */
MPI_Gather(rank_data, NUM_DATA_POINTS, MPI_INT, gathered_data, NUM_DATA_POINTS, MPI_INT, 0, MPI_COMM_WORLD);
Gathering greetings
In the previous episode, we used point-to-point communication to send a greeting message to rank 0 from every other rank. Instead of using point-to-point communication functions, re-implement your solution using
MPI_Gather()instead. You can use this code as your starting point.Solution
#include <mpi.h> #include <stdio.h> #include <stdlib.h> #define NUM_CHARS 32 int main(int argc, char **argv) { int my_rank, num_ranks; MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &my_rank); MPI_Comm_size(MPI_COMM_WORLD, &num_ranks); char message[NUM_CHARS]; snprintf(message, NUM_CHARS, "Hello from rank %d", my_rank); char *recv_buffer = malloc(NUM_CHARS * num_ranks * sizeof(char)); MPI_Gather(message, NUM_CHARS, MPI_CHAR, recv_buffer, NUM_CHARS, MPI_CHAR, 0, MPI_COMM_WORLD); if (my_rank == 0) { for (int i = 0; i < num_ranks; ++i) { // snprintf null terminates strings printf("%s\n", &recv_buffer[i * NUM_CHARS]); } } free(recv_buffer); return MPI_Finalize(); }
Reduce
A reduction operation is one which takes a values across the ranks, and combines them into a single value. Reductions
are probably the most common collective operation you will use. The example at the beginning of this episode was a
reduction operation, summing up a bunch of numbers, implemented using point-to-point communication. Reduction operations
can be done using the collection function MPI_Reduce(), which has the following arguments,
int MPI_Reduce(
void *sendbuf,
void *recvbuffer,
int count,
MPI_Datatype datatype,
MPI_Op op,
int root,
MPI_Comm comm
);
*sendbuf: |
The data to be reduced by the root rank |
*recvbuf: |
A buffer to contain the reduction output |
count: |
The number of elements of data to be reduced |
datatype: |
The data type of the data |
op: |
The reduction operation to perform |
root: |
The root rank, which will perform the reduction |
comm: |
The communicator |
The op argument controls which reduction operation is carried out, from the following possible operations:
| Operation | Description |
|---|---|
MPI_SUM |
Calculate the sum of numbers sent by each rank. |
MPI_MAX |
Return the maximum value of numbers sent by each rank. |
MPI_MIN |
Return the minimum of numbers sent by each rank. |
MPI_PROD |
Calculate the product of numbers sent by each rank. |
MPI_MAXLOC |
Return the maximum value and the number of the rank that sent the maximum value. |
MPI_MINLOC |
Return the minimum value of the number of the rank that sent the minimum value. |
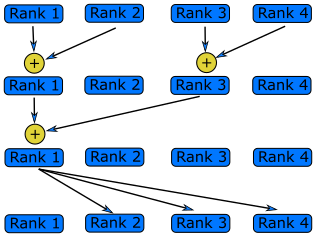
In a reduction operation, each ranks sends a piece of data to the root rank, which are combined, depending on the choice of operation, into a single value on the root rank, as shown in the diagram below. Since the data is sent and operation done on the root rank, it means the reduced value is only available on the root rank.
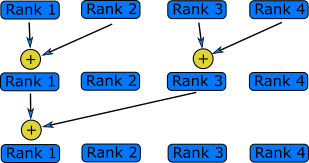
By using MPI_Reduce() and MPI_Bcast(), we can refactor the first code example into two collective functions,
MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
int sum;
MPI_Reduce(&my_rank, &sum, 1, MPI_INT, MPI_SUM, 0, MPI_COMM_WORLD);
MPI_Bcast(&sum, 1, MPI_INT, 0, MPI_COMM_WORLD); /* Using MPI_Bcast to send the reduced value to every rank */
All-to-All
Allreduce
In the code example just above, after the reduction operation we used MPI_Bcast() to communicate the result to every
rank in the communicator. This is a common pattern, so much so that there is a collective operation which does both in a
single function call,
int MPI_Allreduce(
void *sendbuf, /* The data to be reduced */
void *recvbuffer, /* The buffer which will contain the reduction output */
int count, /* The number of elements of data to be reduced */
MPI_Datatype datatype, /* The data type of the data */
MPI_Op op, /* The reduction operation to use */
MPI_Comm comm /* The communicator where the reduction will be performed */
);
*sendbuf: |
The data to be reduced, on all ranks |
*recvbuf: |
A buffer which will contain the reduction output |
count: |
The number of elements of data to be reduced |
datatype: |
The data type of the data |
op: |
The reduction operation to use |
comm: |
The communicator |
MPI_Allreduce() performs the same operations as MPI_Reduce(), but the result is sent to all ranks rather than only
being available on the root rank. This means we can remove the MPI_Bcast() in the previous code example and remove
almost all of the code in the reduction example using point-to-point communication at the beginning of the episode. This
is shown in the following code example.
int sum;
MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
/* MPI_Allreduce effectively replaces all of the code in the first example of this
episode, and is also faster */
MPI_Allreduce(&my_rank, &sum, 1, MPI_INT, MPI_SUM, MPI_COMM_WORLD);
In-place operations
In MPI, we can use in-place operations to eliminate the need for separate send and receive buffers in some collective operations. We typically do this by using the
MPI_IN_PLACEconstant in place of the send buffer, as in the example below usingMPI_Allreduce().sum = my_rank; MPI_Allreduce(MPI_IN_PLACE, &sum, 1, MPI_INT, MPI_SUM, 0, MPI_COMM_WORLD);Not all collective operations support in-place operations, and the usage of
MPI_IN_PLACEcan be different for the other collective functions which support it.
Reductions
The following program creates an array called
vectorthat contains a list ofn_numberson each rank. The first rank contains the numbers from 1 to n_numbers, the second rank from n_numbers to 2*n_numbers and so on. It then calls thefind_maxandfind_sumfunctions that should calculate the sum and maximum of the vector.These functions are not implemented in parallel and only return the sum and the maximum of the local vectors. Modify the
find_sumandfind_maxfunctions to work correctly in parallel usingMPI_ReduceorMPI_Allreduce.#include <stdio.h> #include <mpi.h> // Calculate the sum of numbers in a vector double find_sum(double * vector, int N) { double sum = 0; for (int i = 0; i < N; ++i){ sum += vector[i]; } return sum; } // Find the maximum of numbers in a vector double find_maximum(double *vector, int N) { double max = 0; for (int i = 0; i < N; ++i){ if (vector[i] > max){ max = vector[i]; } } return max; } int main(int argc, char **argv) { int n_numbers = 1024; int rank; double vector[n_numbers]; double sum, max; double my_first_number; // First call MPI_Init MPI_Init(&argc, &argv); // Get my rank MPI_Comm_rank(MPI_COMM_WORLD, &rank); // Each rank will have n_numbers numbers, // starting from where the previous left off my_first_number = n_numbers*rank; // Generate a vector for (int i = 0; i < n_numbers; ++i) { vector[i] = my_first_number + i; } //Find the sum and print sum = find_sum( vector, n_numbers ); printf("The sum of the numbers is %f\n", sum); //Find the maximum and print max = find_maximum( vector, n_numbers ); printf("The largest number is %f\n", max); // Call finalize at the end return MPI_Finalize(); }Solution
// Calculate the sum of numbers in a vector double find_sum(double *vector, int N) { double sum = 0; double global_sum; // Calculate the sum on this rank as before for (int i = 0; i < N; ++i){ sum += vector[i]; } // Call MPI_Allreduce to find the full sum MPI_Allreduce(&sum, &global_sum, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD); return global_sum; } // Find the maximum of numbers in a vector double find_maximum(double *vector, int N) { double max = 0; double global_max; // Calculate the sum on this rank as before for (int i = 0; i < N; ++i){ if (vector[i] > max){ max = vector[i]; } } // Call MPI_Allreduce to find the maximum over all the ranks MPI_Allreduce(&max, &global_max, 1, MPI_DOUBLE, MPI_MAX, MPI_COMM_WORLD); return global_max; }
More collective operations are available
The collective functions introduced in this episode do not represent an exhaustive list of all collective operations in MPI. There are a number which are not covered, as their usage is not as common. You can usually find a list of the collective functions available for the implementation of MPI you choose to use, e.g. Microsoft MPI documentation .
Key Points
Using point-to-point communication to send/receive data to/from all ranks is inefficient
It’s far more efficient to send/receive data to/from multiple ranks by using collective operations