Advanced Communication Techniques

Overview

Teaching: 25 min
Exercises: 20 min

Questions

How do I use complex data structures in MPI?

What is contiguous memory, and why does it matter?

Objectives

Understand the problems of non-contiguous memory in MPI

Know how to define and use derived datatypes

We’ve so far seen the basic building blocks for splitting work and communicating data between ranks, meaning we’re now dangerous enough to write a simple and successful MPI application. We’ve worked, so far, with simple data structures, such as single variables or small 1D arrays. In reality, any useful software we write will use more complex data structures, such as structures, n-dimensional arrays and other complex types. Working with these in MPI require a bit more work to communicate them correctly and efficiently.

To help with this, MPI provides an interface to create new types known as derived datatypes. A derived type acts as a way to enable the translation of complex data structures into instructions which MPI uses for efficient data access communication.

Size limitations for messages

All throughout MPI, the argument which says how many elements of data are being communicated is an integer: int count. In most 64-bit Linux systems, int’s are usually 32-bit and so the biggest number you can pass to count is 2^31 - 1 = 2,147,483,647, which is about 2 billion. Arrays which exceed this length can’t be communicated easily in versions of MPI older than MPI-4.0, when support for “large count” communication was added to the MPI standard. In older MPI versions, there are two workarounds to this limitation. The first is to communicate large arrays in smaller, more manageable chunks. The other is to use derived types, to re-shape the data.

Multi-dimensional arrays

Almost all scientific and computing problems nowadays require us to think in more than one dimension. Using multi-dimensional arrays, such for matrices or tensors, or discretising something onto a 2D or 3D grid of points are fundamental parts for most scientific software. However, the additional dimensions comes with additional complexity, not just in the code we write, but also in how data is communicated.

To create a 2 x 3 matrix, in C, and initialize it with some values, we use the following syntax,

int matrix[2][3] = { {1, 2, 3}, {4, 5, 6} };  // matrix[rows][cols]

This creates an array with two rows and three columns. The first row contains the values {1, 2, 3} and the second row contains {4, 5, 6}. The number of rows and columns can be any value, as long as there is enough memory available.

The importance of memory contiguity

When a sequence of things is contiguous, it means there are multiple adjacent things without anything in between them. In the context of MPI, when we talk about something being contiguous we are almost always talking about how arrays, and other complex data structures, are stored in the computer’s memory. The elements in an array are contiguous when the next, or previous, element are stored in the adjacent memory location.

The memory space of a computer is linear. When we create a multi-dimensional array, the compiler and operating system decide how to map and store the elements into that linear space. There are two ways to do this: row-major or column-major. The difference is which elements of the array are contiguous in memory. Arrays are row-major in C and column-major in Fortran. In a row-major array, the elements in each column of a row are contiguous, so element x[i][j] is preceded by x[i][j - 1] and is followed by x[i][j +1]. In Fortran, arrays are column-major so x(i, j) is followed by x(i + 1, j) and so on.

The diagram below shows how a 4 x 4 matrix is mapped onto a linear memory space, for a row-major array. At the top of the diagram is the representation of the linear memory space, where each number is ID of the element in memory. Below that are two representations of the array in 2D: the left shows the coordinate of each element and the right shows the ID of the element.

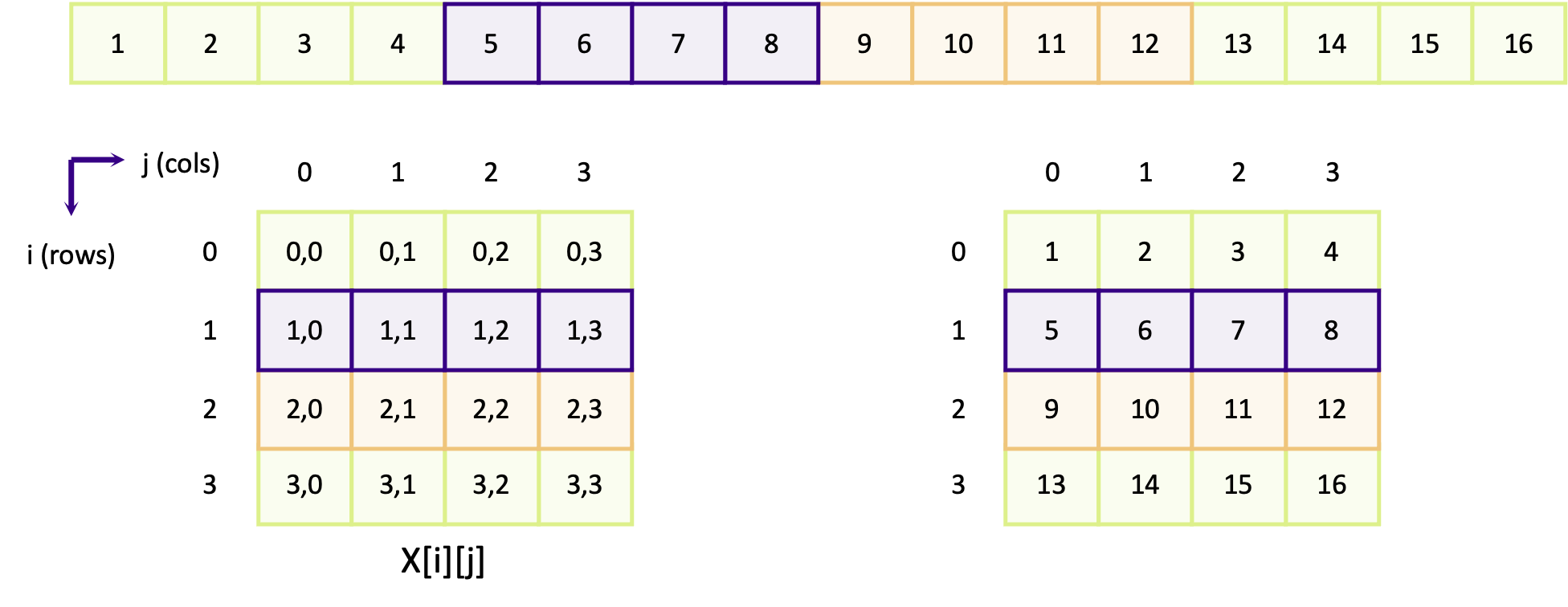
Column memory layout in C

The purple elements (5, 6, 7, 8) which map to the coordinates [1][0], [1][1], [1][2] and [1][3] are contiguous in linear memory. The same applies for the orange boxes for the elements in row 2 (elements 9, 10, 11 and 12). Columns in row-major arrays are contiguous. The next diagram instead shows how elements in adjacent rows are mapped in memory.

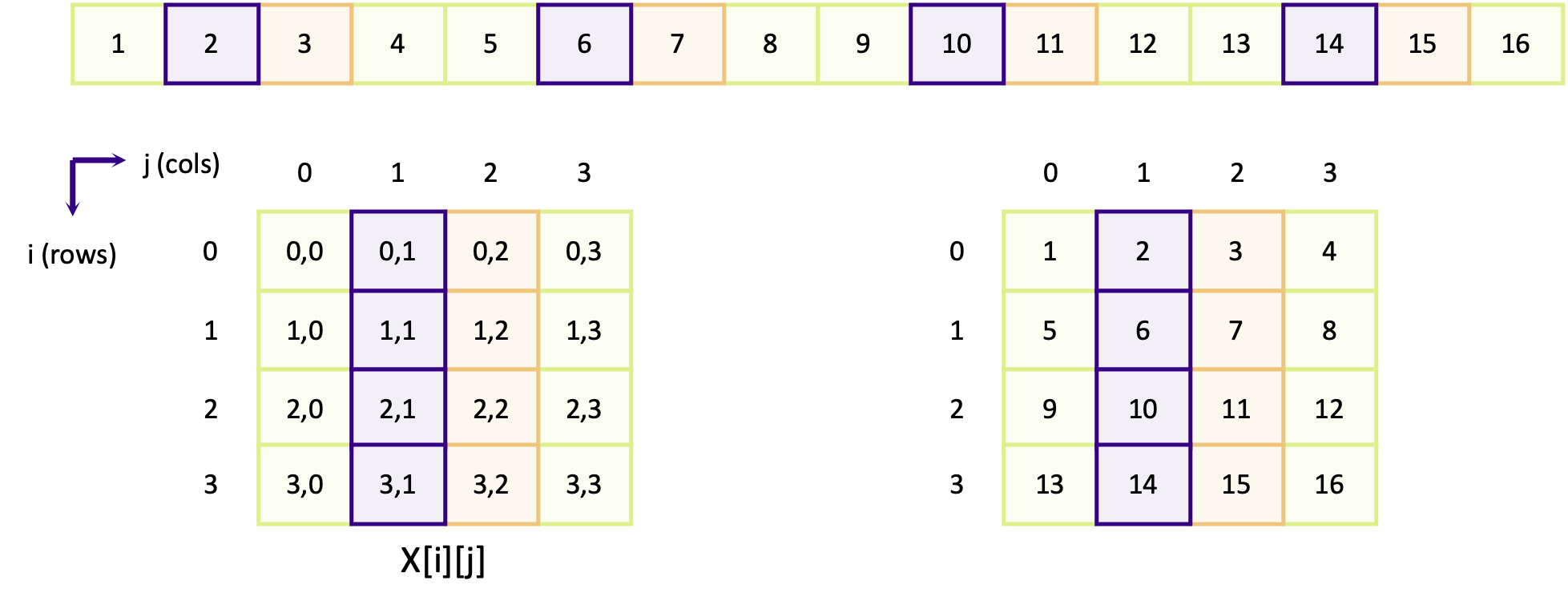
Row memory layout in C

Looking first at the purple boxes (containing elements 2, 6, 10 and 14) which make up the row elements for column 1, we can see that the elements are not contiguous. Element [0][1] maps to element 2 and element [1][1] maps to element 6 and so on. Elements in the same column but in a different row are separated by four other elements, in this example. In other words, elements in other rows are not contiguous.

Does memory contiguity affect performance?

Do you think memory contiguity could impact the performance of our software, in a negative way?

Solution

Yes, memory contiguity can affect how fast our programs run. When data is stored in a neat and organized way, the computer can find and use it quickly. But if the data is scattered around randomly (fragmented), it takes more time to locate and use it, which decreases performance. Keeping our data and data access patterns organized can make our programs faster. But we probably won’t notice the difference for small arrays and data structures.

What about if I use malloc()?

More often than not, we will see malloc() being used to allocate memory for arrays. Especially if the code is using an older standard, such as C90, which does not support variable length arrays. When we use malloc(), we get a contiguous array of elements. To create a 2D array using malloc(), we have to first create an array of pointers (which are contiguous) and allocate memory for each pointer,
int num_rows = 3, num_cols = 5;

float **matrix = malloc(num_rows * sizeof(float*));  /* Each pointer is the start of a row */
for (int i = 0; i < num_rows; ++i) {
   matrix[i] = malloc(num_cols * sizeof(float));     /* Here we allocate memory to store the column elements for row i */
}

for (int i = 0; i < num_rows; ++i) {
   for (int j = 0; i < num_cols; ++j) {
      matrix[i][j] = 3.14159;                        /* Indexing is done as matrix[rows][cols] */
   }
}
There is one problem though. malloc() does not guarantee that subsequently allocated memory will be contiguous. When malloc() requests memory, the operating system will assign whatever memory is free. This is not always next to the block of memory from the previous allocation. This makes life tricky, since data has to be contiguous for MPI communication. But there are workarounds. One is to only use 1D arrays (with the same number of elements as the higher dimension array) and to map the n-dimensional coordinates into a linear coordinate system. For example, the element [2][4] in a 3 x 5 matrix would be accessed as,
int index_for_2_4 = matrix1d[5 * 2 + 4];  // num_cols * row + col
Another solution is to move memory around so that it is contiguous, such as in this example or by using a more sophisticated function such as arralloc() function (not part of the standard library) which can allocate arbitrary n-dimensional arrays into a contiguous block.

For a row-major array, we can send the elements of a single row (for a 4 x 4 matrix) easily,

MPI_Send(&matrix[1][0], 4, MPI_INT ...);

The send buffer is &matrix[1][0], which is the memory address of the first element in row 1. As the columns are four elements long, we have specified to only send four integers. Even though we’re working here with a 2D array, sending a single row of the matrix is the same as sending a 1D array. Instead of using a pointer to the start of the array, an address to the first element of the row (&matrix[1][0]) is used instead. It’s not possible to do the same for a column of the matrix, because the elements down the column are not contiguous.

Using vectors to send slices of an array

To send a column of a matrix, we have to use a vector. A vector is a derived datatype that represents multiple (or one) contiguous sequences of elements, which have a regular spacing between them. By using vectors, we can create data types for column vectors, row vectors or sub-arrays, similar to how we can create slices for Numpy arrays in Python, all of which can be sent in a single, efficient, communication. To create a vector, we create a new datatype using MPI_Type_vector(),

int MPI_Type_vector(
   int count,              /* The number of 'blocks' which makes up the vector */
   int blocklength,        /* The number of contiguous elements in a block */
   int stride,             /* The number of elements between the start of each block */
   MPI_Datatype oldtype,   /* The datatype of the elements of the vector, e.g. MPI_INT, MPI_FLOAT */
   MPI_Datatype *newtype   /* The new datatype which represents the vector  - note that this is a pointer */
);

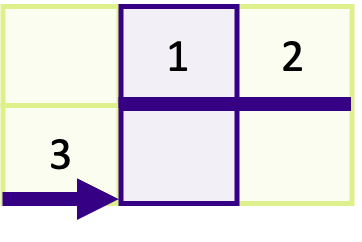
To understand what the arguments mean, look at the diagram below showing a vector to send two rows of a 4 x 4 matrix with a row in between (rows 2 and 4),

How a vector is laid out in memory

A block refers to a sequence of contiguous elements. In the diagrams above, each sequence of contiguous purple or orange elements represents a block. The block length is the number of elements within a block; in the above this is four. The stride is the distance between the start of each block, which is eight in the example. The count is the number of blocks we want. When we create a vector, we’re creating a new derived datatype which includes one or more blocks of contiguous elements.

Before we can use the vector we create to communicate data, it has to be committed using MPI_Type_commit(). This finalises the creation of a derived type. Forgetting to do this step leads to unexpected behaviour, and potentially disastrous consequences!

int MPI_Type_commit(
   MPI_Datatype *datatype  /* The datatype to commit - note that this is a pointer */
);

When a datatype is committed, resources which store information on how to handle it are internally allocated. This contains data structures such as memory buffers as well as data used for bookkeeping. Failing to free those resources after finishing with the vector leads to memory leaks, just like when we don’t free memory created using malloc(). To free up the resources, we use MPI_Type_free(),

int MPI_Type_free (
   MPI_Datatype *datatype  /* The datatype to clean up -- note this is a pointer */
);

The following example code uses a vector to send two rows from a 4 x 4 matrix, as in the example diagram above.

/* The vector is a MPI_Datatype */
MPI_Datatype rows_type;

/* Create the vector type */
const int count = 2;
const int blocklength = 4;
const int stride = 8;
MPI_Type_vector(count, blocklength, stride, MPI_INT, &rows_type);

/* Don't forget to commit it */
MPI_Type_commit(&rows_type);

/* Send the middle row of our 2d matrix array. Note that we are sending
   &matrix[1][0] and not matrix. This is because we are using an offset
   to change the starting point of where we begin sending memory */
int matrix[4][4] = {
   { 1,  2,  3,  4},
   { 5,  6,  7,  8},
   { 9, 10, 11, 12},
   {13, 14, 15, 16},
};

if (my_rank == 0) {
    MPI_Send(&matrix[1][0], 1, rows_type, 1, 0, MPI_COMM_WORLD);
} else {
    /* The receive function doesn't "work" with vector types, so we have to
       say that we are expecting 8 integers instead */
    const int num_elements = count * blocklength;
    int recv_buffer[num_elements];
    MPI_Recv(recv_buffer, num_elements, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}

/* The final thing to do is to free the new datatype when we no longer need it */
MPI_Type_free(&rows_type);

There are two things above, which look quite innocent, but are important to understand. First of all, the send buffer in MPI_Send() is not matrix but &matrix[1][0]. In MPI_Send(), the send buffer is a pointer to the memory location where the start of the data is stored. In the above example, the intention is to only send the second and forth rows, so the start location of the data to send is the address for element [1][0]. If we used matrix, the first and third rows would be sent instead.

The other thing to notice, which is not immediately clear why it’s done this way, is that the receive datatype is MPI_INT and the count is num_elements = count * blocklength instead of a single element of rows_type. This is because when a rank receives data, the data is contiguous array. We don’t need to use a vector to describe the layout of contiguous memory. We are just receiving a contiguous array of num_elements = count * blocklength integers.

Sending columns from an array

Create a vector type to send a column in the following 2 x 3 array:

int matrix[2][3] = {
    {1, 2, 3},
    {4, 5, 6},
 };

With that vector type, send the middle column of the matrix (elements matrix[0][1] and matrix[1][1]) from rank 0 to rank 1 and print the results. You may want to use this code as your starting point.

Solution

If your solution is correct you should see 2 and 5 printed to the screen. In the solution below, to send a 2 x 1 column of the matrix, we created a vector with count = 2, blocklength = 1 and stride = 3. To send the correct column our send buffer was &matrix[0][1] which is the address of the first element in column 1. To see why the stride is 3, take a look at the diagram below,

Stride example for question

You can see that there are three contiguous elements between the start of each block of 1.

#include <mpi.h>
#include <stdio.h>

int main(int argc, char **argv)
{
    int my_rank;
    int num_ranks;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
    MPI_Comm_size(MPI_COMM_WORLD, &num_ranks);

    int matrix[2][3] = {
        {1, 2, 3},
        {4, 5, 6},
    };

    if (num_ranks != 2) {
        if (my_rank == 0) {
            printf("This example only works with 2 ranks\n");
        }
        MPI_Abort(MPI_COMM_WORLD, 1);
    }

    MPI_Datatype col_t;
    MPI_Type_vector(2, 1, 3, MPI_INT, &col_t);
    MPI_Type_commit(&col_t);

    if (my_rank == 0) {
        MPI_Send(&matrix[0][1], 1, col_t, 1, 0, MPI_COMM_WORLD);
    } else {
        int buffer[2];
        MPI_Status status;

        MPI_Recv(buffer, 2, MPI_INT, 0, 0, MPI_COMM_WORLD, &status);

        printf("Rank %d received the following:", my_rank);
        for (int i = 0; i < 2; ++i) {
            printf(" %d", buffer[i]);
        }
        printf("\n");
    }

    MPI_Type_free(&col_t);

    return MPI_Finalize();
}

Sending sub-arrays of an array

By using a vector type, send the middle four elements (6, 7, 10, 11) in the following 4 x 4 matrix from rank 0 to rank 1,
int matrix[4][4] = {
  { 1,  2,  3,  4},
  { 5,  6,  7,  8},
  { 9, 10, 11, 12},
  {13, 14, 15, 16}
};
You can re-use most of your code from the previous exercise as your starting point, replacing the 2 x 3 matrix with the 4 x 4 matrix above and modifying the vector type and communication functions as required.
Solution

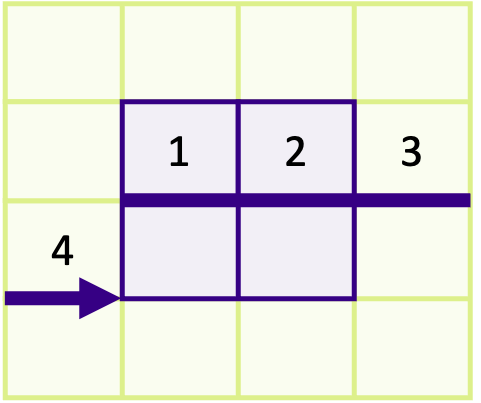
The receiving rank(s) should receive the numbers 6, 7, 10 and 11 if your solution is correct. In the solution below, we have created a vector with a count and block length of 2 and with a stride of 4. The first two arguments means two vectors of block length 2 will be sent. The stride of 4 results from that there are 4 elements between the start of each distinct block as shown in the image below,

You must always remember to send the address for the starting point of the first block as the send buffer, which is why &array[1][1] is the first argument in MPI_Send().
#include <mpi.h>
#include <stdio.h>

int main(int argc, char **argv)
{
    int matrix[4][4] = {
        { 1,  2,  3,  4},
        { 5,  6,  7,  8},
        { 9, 10, 11, 12},
        {13, 14, 15, 16}
    };

    int my_rank;
    int num_ranks;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
    MPI_Comm_size(MPI_COMM_WORLD, &num_ranks);

    if (num_ranks != 2) {
        if (my_rank == 0) {
            printf("This example only works with 2 ranks\n");
        }
        MPI_Abort(MPI_COMM_WORLD, 1);
    }

    MPI_Datatype sub_array_t;
    MPI_Type_vector(2, 2, 4, MPI_INT, &sub_array_t);
    MPI_Type_commit(&sub_array_t);

    if (my_rank == 0) {
        MPI_Send(&matrix[1][1], 1, sub_array_t, 1, 0, MPI_COMM_WORLD);
    } else {
        int buffer[4];
        MPI_Status status;

        MPI_Recv(buffer, 4, MPI_INT, 0, 0, MPI_COMM_WORLD, &status);

        printf("Rank %d received the following:", my_rank);
        for (int i = 0; i < 4; ++i) {
            printf(" %d", buffer[i]);
        }
        printf("\n");
    }

    MPI_Type_free(&sub_array_t);

    return MPI_Finalize();
}

Structures in MPI

Structures, commonly known as structs, are custom datatypes which contain multiple variables of (usually) different types. Some common use cases of structs, in scientific code, include grouping together constants or global variables, or they are used to represent a physical thing, such as a particle, or something more abstract like a cell on a simulation grid. When we use structs, we can write clearer, more concise and better structured code.

To communicate a struct, we need to define a derived datatype which tells MPI about the layout of the struct in memory. Instead of MPI_Type_create_vector(), for a struct, we use, MPI_Type_create_struct(),

int MPI_Type_create_struct(
   int count,                         /* The number of members/fields in the struct */
   int *array_of_blocklengths,        /* The length of the members/fields, as you would use in MPI_Send */
   MPI_Aint *array_of_displacements,  /* The relative positions of each member/field in bytes */
   MPI_Datatype *array_of_types,      /* The MPI type of each member/field */
   MPI_Datatype *newtype,             /* The new derived datatype */
);

The main difference between vector and struct derived types is that the arguments for structs expect arrays, since structs are made up of multiple variables. Most of these arguments are straightforward, given what we’ve just seen for defining vectors. But array_of_displacements is new and unique.

When a struct is created, it occupies a single contiguous block of memory. But there is a catch. For performance reasons, compilers insert arbitrary “padding” between each member for performance reasons. This padding, known as data structure alignment, optimises both the layout of the memory and the access of it. As a result, the memory layout of a struct may look like this instead:

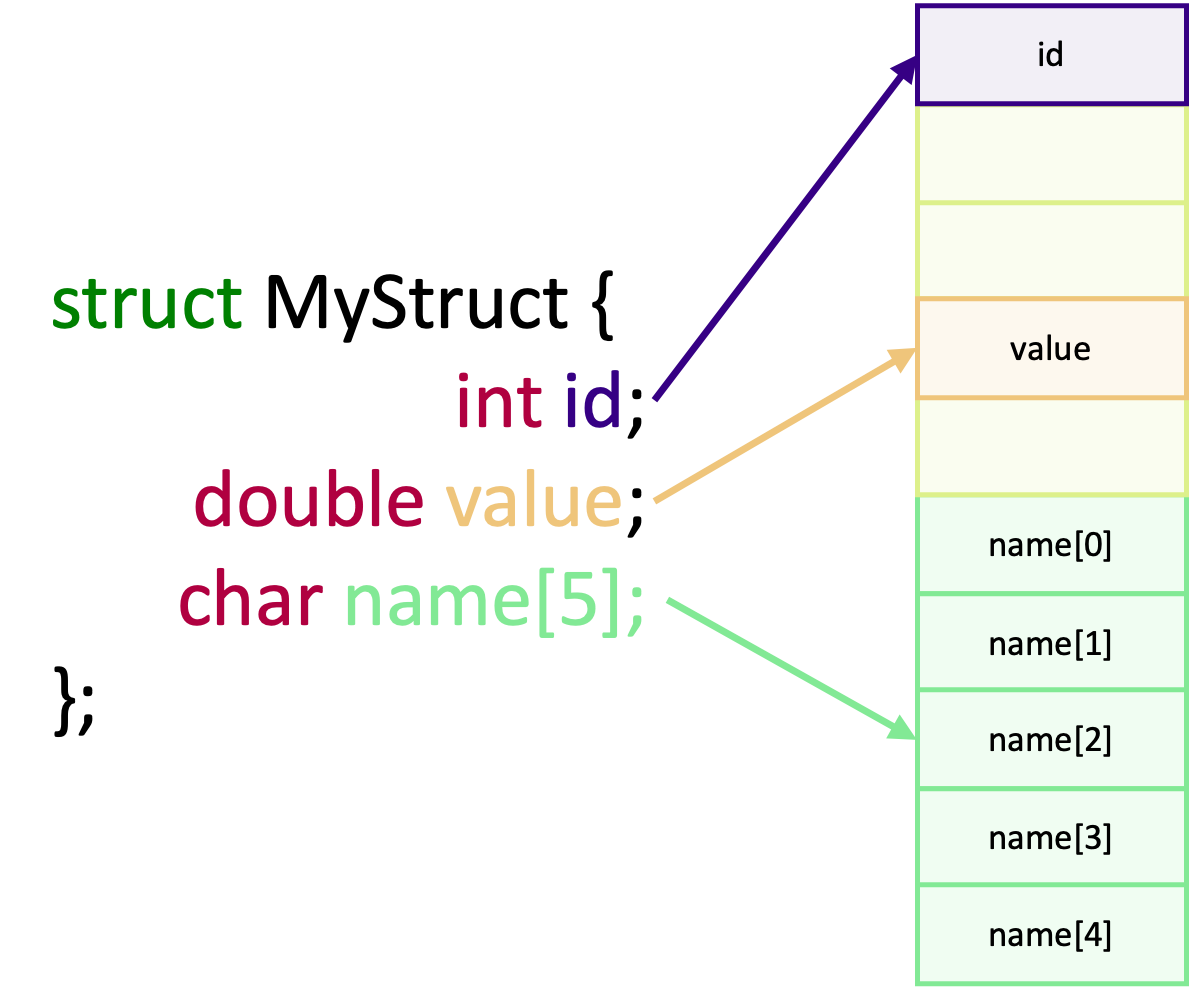
Memory layout for a struct

Although the memory used for padding and the struct’s data exists in a contiguous block, the actual data we care about is not contiguous any more. This is why we need the array_of_displacements argument, which specifies the distance, in bytes, between each struct member relative to the start of the struct. In practise, it serves a similar purpose of the stride in vectors.

To calculate the byte displacement for each member, we need to know where in memory each member of a struct exists. To do this, we can use the function MPI_Get_address(),

int MPI_Get_address{
   const void *location,  /* A pointer to the variable we want the address for */
   MPI_Aint *address,     /* The address of the variable, as an MPI Address Integer -- returned via pointer */
};

In the following example, we use MPI_Type_create_struct() and MPI_Get_address() to create a derived type for a struct with two members,

/* Define and initialize a struct, named foo, with an int and a double */
struct MyStruct {
   int id;
   double value;
} foo = {.id = 0, .value = 3.1459};

/* Create arrays to describe the length of each member and their type */
int count = 2;
int block_lengths[2] = {1, 1};
MPI_Datatype block_types[2] = {MPI_INT, MPI_DOUBLE};

/* Now we calculate the displacement of each member, which are stored in an
   MPI_Aint designed for storing memory addresses */
MPI_Aint base_address;
MPI_Aint block_offsets[2];

MPI_Get_address(&foo, &base_address);            /* First of all, we find the address of the start of the struct */
MPI_Get_address(&foo.id, &block_offsets[0]);     /* Now the address of the first member "id" */
MPI_Get_address(&foo.value, &block_offsets[1]);  /* And the second member "value" */

/* Calculate the offsets, by subtracting the address of each field from the
   base address of the struct */
for (int i = 0; i < 2; ++i) {
   /* MPI_Aint_diff is a macro to calculate the difference between two
      MPI_Aints and is a replacement for:
      (MPI_Aint) ((char *) block_offsets[i] - (char *) base_address) */
   block_offsets[i] = MPI_Aint_diff(block_offsets[i], base_address);
}

/* We finally can create out struct data type */
MPI_Datatype struct_type;
MPI_Type_create_struct(count, block_lengths, block_offsets, block_types, &struct_type);
MPI_Type_commit(&struct_type);

/* Another difference between vector and struct derived types is that in
   MPI_Recv, we use the struct type. We have to do this because we aren't
   receiving a contiguous block of a single type of date. By using the type, we
   tell MPI_Recv how to understand the mix of data types and padding and how to
   assign those back to recv_struct */
if (my_rank == 0) {
   MPI_Send(&foo, 1, struct_type, 1, 0, MPI_COMM_WORLD);
} else {
   struct MyStruct recv_struct;
   MPI_Recv(&recv_struct, 1, struct_type, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}

/* Remember to free the derived type */
MPI_Type_free(&struct_type);

Sending a struct

By using a derived data type, write a program to send the following struct struct Node node from one rank to another,

struct Node {
    int id;
    char name[16];
    double temperature;
};

struct Node node = { .id = 0, .name = "Dale Cooper", .temperature = 42};

You may wish to use this skeleton code as your stating point.

Solution

Your solution should look something like the code block below. When sending a static array (name[16]), we have to use a count of 16 in the block_lengths array for that member.

#include <mpi.h>
#include <stdio.h>

struct Node {
    int id;
    char name[16];
    double temperature;
};

int main(int argc, char **argv)
{
    int my_rank;
    int num_ranks;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
    MPI_Comm_size(MPI_COMM_WORLD, &num_ranks);

    if (num_ranks != 2) {
        if (my_rank == 0) {
            printf("This example only works with 2 ranks\n");
        }
        MPI_Abort(MPI_COMM_WORLD, 1);
    }

    struct Node node = {.id = 0, .name = "Dale Cooper", .temperature = 42};

    int block_lengths[3] = {1, 16, 1};
    MPI_Datatype block_types[3] = {MPI_INT, MPI_CHAR, MPI_DOUBLE};

    MPI_Aint base_address;
    MPI_Aint block_offsets[3];
    MPI_Get_address(&node, &base_address);
    MPI_Get_address(&node.id, &block_offsets[0]);
    MPI_Get_address(&node.name, &block_offsets[1]);
    MPI_Get_address(&node.temperature, &block_offsets[2]);
    for (int i = 0; i < 3; ++i) {
        block_offsets[i] = MPI_Aint_diff(block_offsets[i], base_address);
    }

    MPI_Datatype node_struct;
    MPI_Type_create_struct(3, block_lengths, block_offsets, block_types, &node_struct);
    MPI_Type_commit(&node_struct);

    if (my_rank == 0) {
        MPI_Send(&node, 1, node_struct, 1, 0, MPI_COMM_WORLD);
    } else {
        struct Node recv_node;
        MPI_Recv(&recv_node, 1, node_struct, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
        printf("Received node: id = %d name = %s temperature %f\n", recv_node.id, recv_node.name,
               recv_node.temperature);
    }

    MPI_Type_free(&node_struct);

    return MPI_Finalize();
}

What if I have a pointer in my struct?

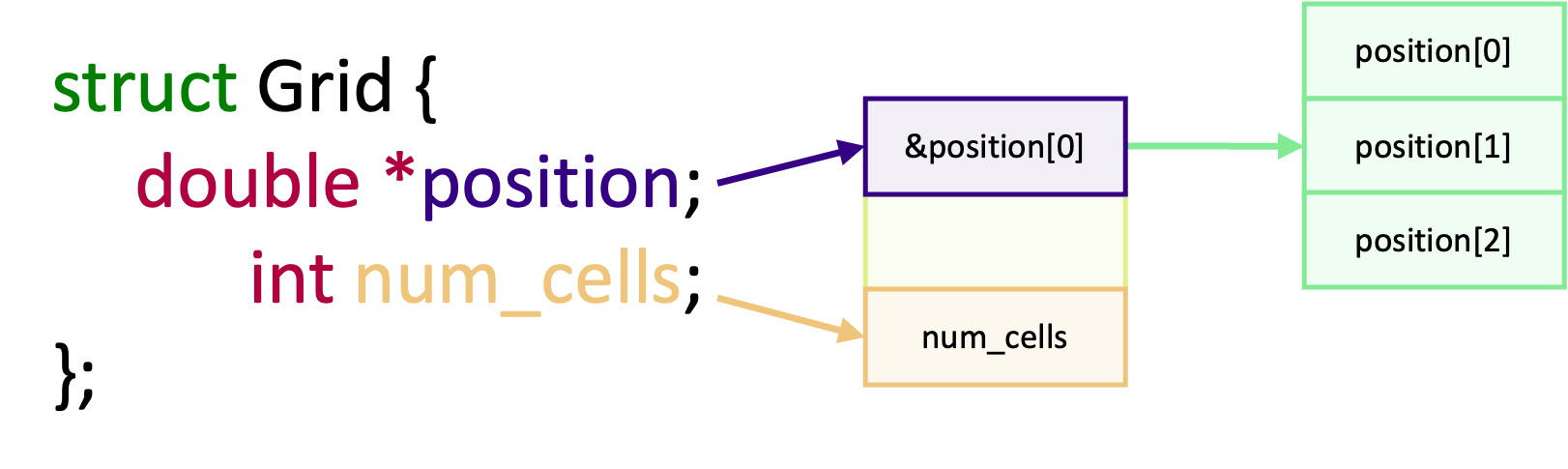
Suppose we have the following struct with a pointer named position and some other fields,
struct Grid {
    double *position;
    int num_cells;
};
grid.position = malloc(3 * sizeof(double));
If we use malloc() to allocate memory for position, how would we send data in the struct and the memory we allocated one rank to another? If you are unsure, try writing a short program to create a derived type for the struct.

Solution

The short answer is that we can’t do it using a derived type, and will have to manually communicate the data separately. The reason why can’t use a derived type is because the address of *position is the address of the pointer. The offset between num_cells and *position is the size of the pointer and whatever padding the compiler adds. It is not the data which position points to. The memory we allocated for *position is somewhere else in memory, as shown in the diagram below, and is non-contiguous with respect to the fields in the struct.

A different way to calculate displacements

There are other ways to calculate the displacement, other than using what MPI provides for us. Another common way is to use the offsetof() macro part of <stddef.h>. offsetof() accepts two arguments, the first being the struct type and the second being the member to calculate the offset for.
#include <stddef.h>
MPI_Aint displacements[2];
displacements[0] = (MPI_Aint) offsetof(struct MyStruct, id);     /* The cast to MPI_Aint is for extra safety */
displacements[1] = (MPI_Aint) offsetof(struct MyStruct, value);
This method and the other shown in the previous examples both returns the same displacement values. It’s mostly a personal choice which you choose to use. Some people prefer the “safety” of using MPI_Get_address() whilst others prefer to write more concise code with offsetof(). Of course, if you’re a Fortran programmer then you can’t use the macro!

Dealing with other non-contiguous data

The previous two sections covered how to communicate complex but structured data between ranks using derived datatypes. However, there are always some edge cases which don’t fit into a derived types. For example, just in the last exercise we’ve seen that pointers and derived types don’t mix well. Furthermore, we can sometimes also reach performance bottlenecks when working with heterogeneous data which doesn’t fit, or doesn’t make sense to be, in a derived type, as each data type needs to be communicated in separate communication calls. This can be especially bad if blocking communication is used! For edge cases situations like this, we can use the MPI_Pack() and MPI_Unpack() functions to do things ourselves.

Both MPI_Pack() and MPI_Unpack() are methods for manually arranging, packing and unpacking data into a contiguous buffer, for cases where regular communication methods and derived types don’t work well or efficiently. They can also be used to create self-documenting message, where the packed data contains additional elements which describe the size, structure and contents of the data. But we have to be careful, as using packed buffers comes with additional overhead, in the form of increased memory usage and potentially more communication overhead as packing and unpacking data is not free.

When we use MPI_Pack(), we take non-contiguous data (sometimes of different datatypes) and “pack” it into a contiguous memory buffer. The diagram below shows how two (non-contiguous) chunks of data may be packed into a contiguous array using MPI_Pack().

Layout of packed memory

The coloured boxes in both memory representations (memory and pakced) are the same chunks of data. The green boxes containing only a single number are used to document the number of elements in the block of elements they are adjacent to, in the contiguous buffer. This is optional to do, but is generally good practise to include to create a self-documenting message. From the diagram we can see that we have “packed” non-contiguous blocks of memory into a single contiguous block. We can do this using MPI_Pack(). To reverse this action, and “unpack” the buffer, we use MPI_Unpack(). As you might expect, MPI_Unpack() takes a buffer, created by MPI_Pack() and unpacks the data back into various memory address.

To pack data into a contiguous buffer, we have to pack each block of data, one by one, into the contiguous buffer using the MPI_Pack() function,

int MPI_Pack(
   const void *inbuf,      /* The data we want to put into the buffer */
   int incount,            /* The number of elements of the buffer */
   MPI_Datatype datatype,  /* The datatype of the elements */
   void *outbuf,           /* The contiguous buffer to pack the data into */
   int outsize,            /* The size of the contiguous buffer, in bytes */
   int *position,          /* A counter of how far into the contiguous buffer to write to */
   MPI_Comm comm           /* The communicator the packed message will be sent using */
);

In the above, inbuf is the data we want to pack into a contiguous buffer and incount and datatype define the number of elements in and the datatype of inbuf. The parameter outbuf is the contiguous buffer the data is packed into, with outsize being the total size of the buffer in bytes. The position argument is used to keep track of the current position, in bytes, where data is being packed into outbuf.

Uniquely, MPI_Pack(), and MPI_Unpack() as well, measure the size of the contiguous buffer, outbuf, in bytes rather than in number of elements. Given that MPI_Pack() is all about manually arranging data, we have to also manage the allocation of memory for outbuf. But how do we allocate memory for it, and how much should we allocate? Allocation is done by using malloc(). Since MPI_Pack() works with outbuf in terms of bytes, the convention is to declare outbuf as a char *. The amount of memory to allocate is simply the amount of space, in bytes, required to store all of the data we want to pack into it. Just like how we would normally use malloc() to create an array. If we had an integer array and a floating point array which we wanted to pack into the buffer, then the size required is easy to calculate,

/* The total buffer size is the sum of the bytes required for the int and float array */
int size_int_array = num_int_elements * sizeof(int);
int size_float_array = num_float_elements * sizeof(float);
int buffer_size = size_int_array + size_float_array;
/* The buffer is a char *, but could also be cast as void * if you prefer */
char *buffer = malloc(buffer_size * sizeof(char));  // a char is 1 byte, so sizeof(char) is optional

If we are also working with derived types, such as vectors or structs, then we need to find the size of those types. By far the easiest way to handle these is to use MPI_Pack_size(), which supports derived datatypes through the MPI_Datatype,

int MPI_Pack_size(
   int incount,            /* The number of elements in the data */
   MPI_Datatype datatype,  /* The datatype of the data*/
   MPI_Comm comm,          /* The communicator the data will be sent over */
   int *size               /* The calculated upper size limit for the buffer, in bytes */
);

MPI_Pack_size() is a helper function to calculate the upper bound of memory required. It is, in general, preferable to calculate the buffer size using this function, as it takes into account any implementation specific MPI detail and thus is more portable between implementations and systems. If we wanted to calculate the memory required for three elements of some derived struct type and a double array, we would do the following,

int struct_array_size, float_array_size;
MPI_Pack_size(3, STRUCT_DERIVED_TYPE, MPI_COMM_WORLD, &struct_array_size);
MPI_Pack_size(50, MPI_DOUBLE. MPI_COMM_WORLD, &float_array_size);
int buffer_size = struct_array_size + float_array_size;

When a rank has received a contiguous buffer, it has to be unpacked into its constituent parts, one by one, using MPI_Unpack(),

int MPI_Unpack(
   const void *inbuf,      /* The contiguous buffer to unpack */
   int insize,             /* The total size of the buffer, in bytes */
   int *position,          /* The position, in bytes, for where to start unpacking from */
   void *outbuf,           /* An array, or variable, to unpack data into -- this is the output */
   int outcount,           /* The number of elements of data to unpack */
   MPI_Datatype datatype,  /* The datatype of the elements to unpack */
   MPI_Comm comm,          /* The communicator the message was sent using */
);

The arguments for this function are essentially the reverse of MPI_Pack(). Instead of being the buffer to pack into, inbuf is now the packed buffer and position is the position, in bytes, in the buffer where to unpacking from. outbuf is then the variable we want to unpack into, and outcount is the number of elements of datatype to unpack.

In the example below, MPI_Pack(), MPI_Pack_size() and MPI_Unpack() are used to communicate a (non-contiguous) 3 x 3 matrix.

/* Allocate and initialise a (non-contiguous) 2D matrix that we will pack into
   a buffer */
int num_rows = 3, num_cols = 3;
int **matrix = malloc(num_rows * sizeof(int *));
for (int i = 0; i < num_rows; ++i) {
   matrix[i] = malloc(num_cols * sizeof(int));
   for (int j = 0; i < num_cols; ++j) {
      matrix[i][j] = num_cols * i + j;
   }
}

/* Determine the upper limit for the amount of memory the buffer requires. Since
   this is a simple situation, we could probably have done this manually using
   `num_rows * num_cols * sizeof(int)`. The size `pack_buffer_size` is returned in
   bytes */
int pack_buffer_size;
MPI_Pack_size(num_rows * num_cols, MPI_INT, MPI_COMM_WORLD, &pack_buffer_size);

if (my_rank == 0) {
    /* Create the pack buffer and pack each row of data into it buffer
       one by one */
    int position = 0;
    char *packed_data = malloc(pack_buffer_size);
    for (int i = 0; i < num_rows; ++i) {
        MPI_Pack(matrix[i], num_cols, MPI_INT, packed_data, pack_buffer_size, &position, MPI_COMM_WORLD);
    }

    /* Send the packed data to rank 1 */
    MPI_Send(packed_data, pack_buffer_size, MPI_PACKED, 1, 0, MPI_COMM_WORLD);
} else {
    /* Create a receive buffer and get the packed buffer from rank 0 */
    char *received_data = malloc(pack_buffer_size);
    MPI_Recv(received_data, pack_buffer_size + 1, MPI_PACKED, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);

    /* allocate a matrix to put the receive buffer into -- this is for
       demonstration purposes */
    int **my_matrix = malloc(num_rows * sizeof(int *));
    for (int i = 0; i < num_cols; ++i) {
        my_matrix[i] = malloc(num_cols * sizeof(int));
    }

    /* Unpack the received data row by row into my_matrix */
    int position = 0;
    for (int i = 0; i < num_rows; ++i) {
        MPI_Unpack(received_data, pack_buffer_size, &position, my_matrix[i], num_cols, MPI_INT, MPI_COMM_WORLD);
    }
}

Blocking or non-blocking?

The processes of packing data into a contiguous buffer does not happen asynchronously. The same goes for unpacking data. But this doesn’t restrict the packed data from being only sent synchronously. The packed data can be communicated using any communication function, just like the previous derived types. It works just as well to communicate the buffer using non-blocking methods, as it does using blocking methods.

What if the other rank doesn’t know the size of the buffer?

In some cases, the receiving rank may not know the size of the buffer used in MPI_Pack(). This could happen if a message is sent and received in different functions, if some ranks have different branches through the program or if communication happens in a dynamic or non-sequential way.

In these situations, we can use MPI_Probe() and MPI_Get_count to find the a message being sent and to get the number of elements in the message.
/* First probe for a message, to get the status of it */
MPI_Status status;
MPI_Probe(0, 0, MPI_COMM_WORLD, &status);
/* Using MPI_Get_count we can get the number of elements of a particular data type */
int message_size;
MPI_Get_count(&status, MPI_PACKED, &buffer_size);
/* MPI_PACKED represents an element of a "byte stream." So, buffer_size is the size of the buffer to allocate */
char *buffer = malloc(buffer_size);

Sending heterogeneous data in a single communication

Suppose we have two arrays below, where one contains integer data and the other floating point data. Normally we would use multiple communication calls to send each type of data individually, for a known number of elements. For this exercise, communicate both arrays using a packed memory buffer.

int int_data_count = 5;
int float_data_count = 10;

int   *int_data = malloc(int_data_count * sizeof(int));
float *float_data = malloc(float_data_count * sizeof(float));

/* Initialize the arrays with some values */
for (int i = 0; i < int_data_count; ++i) {
  int_data[i] = i + 1;
}
for (int i = 0; i < float_data_count; ++i) {
  float_data[i] = 3.14159 * (i + 1);
}

Since the arrays are dynamically allocated, in rank 0, you should also pack the number of elements in each array. Rank 1 may also not know the size of the buffer. How would you deal with that?

You can use this skeleton code to begin with.

Solution

The additional restrictions for rank 1 not knowing the size of the arrays or packed buffer add some complexity to receiving the packed buffer from rank 0.

#include <mpi.h>
#include <stdio.h>
#include <stdlib.h>

int main(int argc, char **argv)
{
    int my_rank;
    int num_ranks;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
    MPI_Comm_size(MPI_COMM_WORLD, &num_ranks);

    if (num_ranks != 2) {
        if (my_rank == 0) {
            printf("This example only works with 2 ranks\n");
        }
        MPI_Abort(MPI_COMM_WORLD, 1);
    }

    if (my_rank == 0) {
        int int_data_count = 5, float_data_count = 10;
        int *int_data = malloc(int_data_count * sizeof(int));
        float *float_data = malloc(float_data_count * sizeof(float));
        for (int i = 0; i < int_data_count; ++i) {
            int_data[i] = i + 1;
        }
        for (int i = 0; i < float_data_count; ++i) {
            float_data[i] = 3.14159 * (i + 1);
        }

        /* use MPI_Pack_size to determine how big the packed buffer needs to be */
        int buffer_size_count, buffer_size_int, buffer_size_float;
        MPI_Pack_size(2, MPI_INT, MPI_COMM_WORLD, &buffer_size_count); /* 2 * INT because we will have 2 counts*/
        MPI_Pack_size(int_data_count, MPI_INT, MPI_COMM_WORLD, &buffer_size_int);
        MPI_Pack_size(float_data_count, MPI_FLOAT, MPI_COMM_WORLD, &buffer_size_float);
        int total_buffer_size = buffer_size_int + buffer_size_float + buffer_size_count;

        int position = 0;
        char *buffer = malloc(total_buffer_size);

        /* Pack the data size, followed by the actually data */
        MPI_Pack(&int_data_count, 1, MPI_INT, buffer, total_buffer_size, &position, MPI_COMM_WORLD);
        MPI_Pack(int_data, int_data_count, MPI_INT, buffer, total_buffer_size, &position, MPI_COMM_WORLD);
        MPI_Pack(&float_data_count, 1, MPI_INT, buffer, total_buffer_size, &position, MPI_COMM_WORLD);
        MPI_Pack(float_data, float_data_count, MPI_FLOAT, buffer, total_buffer_size, &position, MPI_COMM_WORLD);

        /* buffer is sent in one communication using MPI_PACKED */
        MPI_Send(buffer, total_buffer_size, MPI_PACKED, 1, 0, MPI_COMM_WORLD);

        free(buffer);
        free(int_data);
        free(float_data);
    } else {
        int buffer_size;
        MPI_Status status;
        MPI_Probe(0, 0, MPI_COMM_WORLD, &status);
        MPI_Get_count(&status, MPI_PACKED, &buffer_size);

        char *buffer = malloc(buffer_size);
        MPI_Recv(buffer, buffer_size, MPI_PACKED, 0, 0, MPI_COMM_WORLD, &status);

        int position = 0;
        int int_data_count, float_data_count;

        /* Unpack an integer why defines the size of the integer array,
        then allocate space for an unpack the actual array */
        MPI_Unpack(buffer, buffer_size, &position, &int_data_count, 1, MPI_INT, MPI_COMM_WORLD);
        int *int_data = malloc(int_data_count * sizeof(int));
        MPI_Unpack(buffer, buffer_size, &position, int_data, int_data_count, MPI_INT, MPI_COMM_WORLD);

        MPI_Unpack(buffer, buffer_size, &position, &float_data_count, 1, MPI_INT, MPI_COMM_WORLD);
        float *float_data = malloc(float_data_count * sizeof(float));
        MPI_Unpack(buffer, buffer_size, &position, float_data, float_data_count, MPI_FLOAT, MPI_COMM_WORLD);

        printf("int data: [");
        for (int i = 0; i < int_data_count; ++i) {
            printf(" %d", int_data[i]);
        }
        printf(" ]\n");

        printf("float data: [");
        for (int i = 0; i < float_data_count; ++i) {
            printf(" %f", float_data[i]);
        }
        printf(" ]\n");

        free(int_data);
        free(float_data);
        free(buffer);
    }

    return MPI_Finalize();
}

Key Points

Communicating complex, heterogeneous or non-contiguous data structures in MPI requires a bit more work

Any data being transferred should be a single contiguous block of memory

By defining derived datatypes, we can easily send data which is not contiguous

The functions MPI_Pack and MPI_Unpack can be used to manually create a contiguous memory block of data

previous episode

next episode

Advanced Communication Techniques

Overview

Size limitations for messages

Multi-dimensional arrays

The importance of memory contiguity

Does memory contiguity affect performance?

Solution

What about if I use `malloc()`?

Using vectors to send slices of an array

Sending columns from an array

Solution

Sending sub-arrays of an array

Solution

Structures in MPI

Sending a struct

Solution

What if I have a pointer in my struct?

Solution

A different way to calculate displacements

Dealing with other non-contiguous data

Blocking or non-blocking?

What if the other rank doesn’t know the size of the buffer?

Sending heterogeneous data in a single communication

Solution

Key Points

previous episode

next episode

previous episode

next episode

Advanced Communication Techniques

Overview

Size limitations for messages

Multi-dimensional arrays

The importance of memory contiguity

Does memory contiguity affect performance?

Solution

What about if I use malloc()?

Using vectors to send slices of an array

Sending columns from an array

Solution

Sending sub-arrays of an array

Solution

Structures in MPI

Sending a struct

Solution

What if I have a pointer in my struct?

Solution

A different way to calculate displacements

Dealing with other non-contiguous data

Blocking or non-blocking?

What if the other rank doesn’t know the size of the buffer?

Sending heterogeneous data in a single communication

Solution

Key Points

previous episode

next episode

What about if I use `malloc()`?